题目内容
在正方体ABCD-A1B1C1D1中，下列命题：
①（
+
+
）2=3
2；
②
•(
-
)=0；
③
与
的夹角为60°；
④正方体的体积为|
•
•
|．
其中正确的命题的序号是 ．
①（
| AA1 |
| AD |
| AB |
| AB |
②
| A1C |
| A1B1 |
| A1A |
③
| AD1 |
| A1B |
④正方体的体积为|
| AB |
| AA1 |
| AD |
其中正确的命题的序号是
考点：棱柱的结构特征
专题：空间向量及应用
分析：首先，结合图形，以点D为坐标原点，以向量
，
，
所在直线分别为x，y，z轴，建立空间直角坐标系，
设棱长为1，则D（0，0，0），A（1，0，0），B（1，1，0），C（0，1，0），A1（1，0，1），B1（1，1，1），C1（0，1，1），D1（0，0，1），然后，结合空间向量的坐标运算，对四个命题进行逐个检验即可．
| DA |
| DC |
| DD1 |
设棱长为1，则D（0，0，0），A（1，0，0），B（1，1，0），C（0，1，0），A1（1，0，1），B1（1，1，1），C1（0，1，1），D1（0，0，1），然后，结合空间向量的坐标运算，对四个命题进行逐个检验即可．
解答：
解：如图所示：
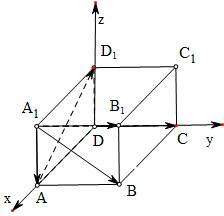
以点D为坐标原点，以向量
，
，
所在直线分别为x，y，z轴，建立空间直角坐标系，
设棱长为1，则D（0，0，0），A（1，0，0），B（1，1，0），C（0，1，0），
A1（1，0，1），B1（1，1，1），C1（0，1，1），D1（0，0，1），
对于①：
+
=
，
∴
=(-1，0，1)，
=(0，1，0)，
∴
+
=(-1，1，1)，
∴|
+
|=
，|
|=1，
∴①正确；
对于②：
=(-1，1，1)
=(0，1，0)，
=(0，0，-1)，
∴
•(
-
)=2．
∴②错误；
对于③：
=(-1，0，0)，
=(0，1，-1)，
∴
•
=0，
∴③正确；
对于④：
∵
•
=0，
∴④错误，
综上，正确的命题为：①③，
故答案为：①③．
以点D为坐标原点，以向量
| DA |
| DC |
| DD1 |
设棱长为1，则D（0，0，0），A（1，0，0），B（1，1，0），C（0，1，0），
A1（1，0，1），B1（1，1，1），C1（0，1，1），D1（0，0，1），
对于①：
| AA1 |
| AD |
| AD1 |
∴
| AD1 |
| AB |
∴
| AD1 |
| AB |
∴|
| AD1 |
| AB |
| 3 |
| AB |
∴①正确；
对于②：
| A1C |
| A1B1 |
| A1A |
∴
| A1C |
| A1B1 |
| A1A |
∴②错误；
对于③：
| AD1 |
| A1B |
∴
| AD1 |
| A1B |
∴③正确；
对于④：
∵
| AB |
| AA1 |
∴④错误，
综上，正确的命题为：①③，
故答案为：①③．
点评：本题重点考查了空间直角坐标系、空间向量的坐标表示和运算，属于中档题．
练习册系列答案
相关题目
如图甲，在平面四边形PABC中，PA=AC=2，∠P=45°，∠B=90°，将一颗质地均匀的骰子连续抛掷三次，依次得到的三个点数成等差数列的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|