题目内容
已知F1,F2分别是双曲线
-
=1的左、右焦点,P为双曲线右支上的任意一点,则
的最小值为( )
| x2 |
| 4 |
| y2 |
| 21 |
| |PF1|2 |
| |PF2| |
| A、24 | B、20 | C、16 | D、12 |
考点:双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:首先利用双曲线的定义求出关系式,进一步利用均值不等式建立关系式,
=
,最后求出结果.
|
| ||
|
|
| (4+n)2 |
| n |
解答:
解:设|PF2|=n,(n≥3)
则:根据双曲线的定义:|PF1|=4+n,
则
=
=n+
+8≥2
+8=16,
当且仅当n=4时成立.
故
的最小值为16,
故选:C
则:根据双曲线的定义:|PF1|=4+n,
则
| |PF1|2 |
| |PF2| |
| (4+n)2 |
| n |
| 16 |
| n |
n•
|
当且仅当n=4时成立.
故
| |PF1|2 |
| |PF2| |
故选:C
点评:本题考查的知识要点:双曲线的定义的应用.双曲线的离心率,均值不等式的应用,属于中等题型.

练习册系列答案
相关题目
在正项等比数列{an}中,lga3+lga6+lga9=6,则a5•a7的值是( )
| A、10000 | B、1000 |
| C、100 | D、10 |
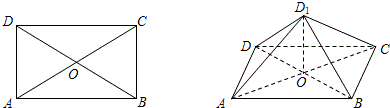
 如图甲,在平面四边形PABC中,PA=AC=2,∠P=45°,∠B=90°,
如图甲,在平面四边形PABC中,PA=AC=2,∠P=45°,∠B=90°,