题目内容
已知命题p:x1和x2是方程x2-mx-2=0的两个实根,不等式a2-5a-3≥|x1-x2|对任意实数m∈[-1,1]恒成立;命题q:方程a2x2+ax-2=0在[-1,1]上有解.若命题p是假命题且命题q是真命题,求实数a的取值范围.
考点:复合命题的真假,函数恒成立问题
专题:简易逻辑
分析:命题p:|x1-x2|=
≤3,所以可以得到a2-5a-3≥3,解该不等式即得a≤-1,或a≥6;
命题q:a2x2+ax-2=(ax-1)(ax+2)=0,所以x=
,或-
,所以有|
|≤1,或|-
|≤1,这样即可求出a的取值范围:a≤-1,或a≥1;
根据命题p是假命题且命题q是真命题可得
,解该不等式即可得到a的取值范围.
| m2+8 |
命题q:a2x2+ax-2=(ax-1)(ax+2)=0,所以x=
| 1 |
| a |
| 2 |
| a |
| 1 |
| a |
| 2 |
| a |
根据命题p是假命题且命题q是真命题可得
|
解答:
解:∵x1,x2是方程x2-mx-2=0的两实根;
∴
;
∴|x1-x2|=
=
;
当m∈[-1,1]时,|x1-x2|max=3;
由不等式a2-5a-3≥|x1-x2|对任意实数m∈[-1,1]恒成立可得:
a2-5a-3≥3,解得a≤-1,或a≥6,∴命题p为真时,a满足a≤-1,或a≥6;
对于方程a2x2+ax-2=0显然a≠0,并解该方程得x=-
,或
;
∵该方程在[-1,1]上有解,则:|-
|≤1,或|
|≤1,∴|a|≤1,即a≤-1,或a≥1;
∵命题p是假命题,且命题q是真命题;
∴
,解得1≤a<6;
∴实数a的取值范围是[1,6).
∴
|
∴|x1-x2|=
| (x1+x2)2-4x1x2 |
| m2+8 |
当m∈[-1,1]时,|x1-x2|max=3;
由不等式a2-5a-3≥|x1-x2|对任意实数m∈[-1,1]恒成立可得:
a2-5a-3≥3,解得a≤-1,或a≥6,∴命题p为真时,a满足a≤-1,或a≥6;
对于方程a2x2+ax-2=0显然a≠0,并解该方程得x=-
| 2 |
| a |
| 1 |
| a |
∵该方程在[-1,1]上有解,则:|-
| 2 |
| a |
| 1 |
| a |
∵命题p是假命题,且命题q是真命题;
∴
|
∴实数a的取值范围是[1,6).
点评:考查韦达定理,二次函数的最值,解一元二次不等式,及真命题,假命题的概念.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
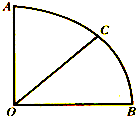 如图,在圆心角为90°的扇形中以圆心.为起点作射线OC,则使得∠AOC与∠BOC都不大于60°的概率是( )
如图,在圆心角为90°的扇形中以圆心.为起点作射线OC,则使得∠AOC与∠BOC都不大于60°的概率是( )A、
| ||
B、
| ||
C、
| ||
D、
|
若f(x)=cosx在[-b,-a]上是增函数,则f(x)在[a,b]上是( )
| A、奇函数 | B、偶函数 |
| C、减函数 | D、增函数 |
已知cosα=-
,且π<α<
,则tanα=( )
| 5 |
| 13 |
| 3π |
| 2 |
A、-
| ||
B、
| ||
C、-
| ||
D、
|
