题目内容
已知圆C经过P(4,-2),Q(-1,3)两点,圆心C在第一象限且到直线3x+4y+4=0的距离为
.
(I)求直线PQ与圆C的方程;
(Ⅱ)是否存在直线l∥PQ,使得直线l与圆C交于点A、B,且以AB为直径的圆经过坐标原点,若存在求出直线l的方程,不存在说明理由.
| 14 |
| 5 |
(I)求直线PQ与圆C的方程;
(Ⅱ)是否存在直线l∥PQ,使得直线l与圆C交于点A、B,且以AB为直径的圆经过坐标原点,若存在求出直线l的方程,不存在说明理由.
考点:直线与圆相交的性质
专题:综合题,直线与圆
分析:(I)利用点斜式求直线PQ,求出圆心与半径,可得圆C的方程;
(Ⅱ)假设直线l存在,设方程为x+y+m=0,代入圆方程,利用以AB为直径的圆经过坐标原点O,可得AO⊥BO,即x1x2+y1y2=0,从而可得直线l的方程.
(Ⅱ)假设直线l存在,设方程为x+y+m=0,代入圆方程,利用以AB为直径的圆经过坐标原点O,可得AO⊥BO,即x1x2+y1y2=0,从而可得直线l的方程.
解答:
解:(I)PQ直线方程:y+2=
(x-4)即x+y-2=0
∵C在PQ的中垂线上,PQ的中垂线方程为y-
=x-
即y=x-1
设C(a,a-1),由条件d=
=
得|a|=2
∵圆心C在第一象限,∴a=2,即C(2,1)
所以圆C的方程为:(x-2)2+(y-1)2=13
(Ⅱ)假设存在l与圆C交于点A(x1,y1)、B(x2,y2),且以AB为直径的圆经过坐标原点,
其方程设为x+y+m=0代人圆C方程得2x2+2(m-1)x+m2+2m-8=0△=4(m-1)2-8(m2+2m-8)>0得-3-
<m<-3+
(*)x1+x2=1-m,x1x2=
;
∵OA⊥OB,∴x1x2+y1y2=0可得2x1x2+m(x1+x2)+m2=0
可得m2+3m-8=0解得m=
满足(*)
∴直线l的方程为:2x+2y-3+
=0和2x+2y-3-
=0.
| 3+2 |
| -1-5 |
∵C在PQ的中垂线上,PQ的中垂线方程为y-
| 1 |
| 2 |
| 3 |
| 2 |
设C(a,a-1),由条件d=
| |3a+4(a-1)+4| |
| 5 |
| 14 |
| 5 |
∵圆心C在第一象限,∴a=2,即C(2,1)
所以圆C的方程为:(x-2)2+(y-1)2=13
(Ⅱ)假设存在l与圆C交于点A(x1,y1)、B(x2,y2),且以AB为直径的圆经过坐标原点,
其方程设为x+y+m=0代人圆C方程得2x2+2(m-1)x+m2+2m-8=0△=4(m-1)2-8(m2+2m-8)>0得-3-
| 26 |
| 26 |
| m2+2m-8 |
| 2 |
∵OA⊥OB,∴x1x2+y1y2=0可得2x1x2+m(x1+x2)+m2=0
可得m2+3m-8=0解得m=
-3±
| ||
| 2 |
∴直线l的方程为:2x+2y-3+
| 41 |
| 41 |
点评:本题考查直线与圆的位置关系,考查学生对直线与圆相交的问题的转化方法,考查学生的方程思想和运算化简能力,属于中档题.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案
相关题目
已知sinα-cosα=
,则tanα等于( )
| 2 |
| A、-1 | ||||
B、-
| ||||
C、
| ||||
| D、1 |
下列各组函数f(x)与g(x)的图象相同的是( )
A、f(x)=x,g(x)=(
| ||||||||||
| B、f(x)=x2,g(x)=(x+1)2 | ||||||||||
C、f(x)=1,g(x)=
| ||||||||||
D、f(x)=|x|,g(x)=
|
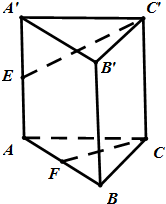 已知三棱柱ABC-A′B′C′,侧棱与底面垂直,且所有的棱长均为2,E为AA′的中点,F为AB的中点.
已知三棱柱ABC-A′B′C′,侧棱与底面垂直,且所有的棱长均为2,E为AA′的中点,F为AB的中点.


