题目内容
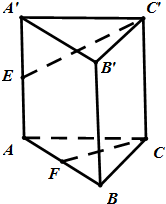 已知三棱柱ABC-A′B′C′,侧棱与底面垂直,且所有的棱长均为2,E为AA′的中点,F为AB的中点.
已知三棱柱ABC-A′B′C′,侧棱与底面垂直,且所有的棱长均为2,E为AA′的中点,F为AB的中点.(Ⅰ)求多面体ABCB′C′E的体积;
(Ⅱ)求异面直线C'E与CF所成角的余弦值.
考点:异面直线及其所成的角,棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:(I)分别求出直三棱柱ABC-A′B′C′的体积V.三棱锥E-A′B′C′的体积V1.即可得出多面体ABCB′C′E的体积=V-V1;
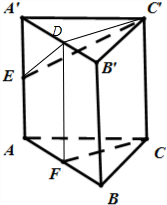
(II)如图所示,取A′B′的中点D,连接C′D,DF,DE.可得四边形CFDC′是矩形.C′D∥CF.因此∠EC′D即是异面直线C′E与CF所成角.
(II)如图所示,取A′B′的中点D,连接C′D,DF,DE.可得四边形CFDC′是矩形.C′D∥CF.因此∠EC′D即是异面直线C′E与CF所成角.
解答:
解:(I)直三棱柱ABC-A′B′C′的体积V=
×22×2=2
.
三棱锥E-A′B′C′的体积V1=
S△A′B′C′•A′E=
×
×22×1=
.
∴多面体ABCB′C′E的体积=V-V1=
;
(II)如图所示,取A′B′的中点D,连接C′D,DF,DE.
可得四边形CFDC′是矩形.
∴C′D∥CF.
∴∠EC′D即是异面直线C′E与CF所成角.
在Rt△C′DE中,C′D=
,C′E=
.
∴cos∠EC′D=
=
=
.
∴异面直线C′E与CF所成角的余弦值为
.
| ||
| 4 |
| 3 |

三棱锥E-A′B′C′的体积V1=
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 4 |
| ||
| 3 |
∴多面体ABCB′C′E的体积=V-V1=
5
| ||
| 3 |
(II)如图所示,取A′B′的中点D,连接C′D,DF,DE.
可得四边形CFDC′是矩形.
∴C′D∥CF.
∴∠EC′D即是异面直线C′E与CF所成角.
在Rt△C′DE中,C′D=
| 3 |
| 5 |
∴cos∠EC′D=
| C′D |
| C′E |
| ||
|
| ||
| 5 |
∴异面直线C′E与CF所成角的余弦值为
| ||
| 5 |
点评:本题考查了直三棱柱的体积及其性质、异面直线所成的角、直角三角形的边角关系,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
不透明的盒子里面装有五个分别标有数字1、2、3、4、5的乒乓球,这些球除数字外,其他完全相同,一位学生随机摸出两个球,两个球的数字之和是偶数的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
函数f(x)=x2-2|x|-m的零点有两个,求实数m的取值范围( )
| A、-1<m<0 |
| B、m>0或m=-1 |
| C、m>0 或-1≤m<0 |
| D、0<m<1 |