题目内容
19.已知椭圆的焦点是F1(-1,0)和F2(1,0),离心率$e=\frac{1}{2}$.(Ⅰ)求椭圆的方程;
(Ⅱ)设点P是椭圆上一点,且∠F1PF2=60°,求△F1PF2的面积.
分析 (Ⅰ)由已知可得c,再由离心率求得a,结合隐含条件求得b,则椭圆方程可求;
(Ⅱ)在焦点三角形中利用余弦定理求得|PF1||PF2|,代入三角形面积公式得答案.
解答 解:(Ⅰ)由题意可设椭圆方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1(a>b>0)$,
且c=1,又$e=\frac{c}{a}=\frac{1}{2}$,得a=2,
∴b2=a2-c2=4-1=3,
∴椭圆的方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$;
(Ⅱ)在△PF1F2中,由余弦定理可得:$4{c}^{2}=|P{F}_{1}{|}^{2}+|P{F}_{2}{|}^{2}-2|P{F}_{1}||P{F}_{2}|cos$∠F1PF2,
即$4=(|P{F}_{1}|+|P{F}_{2}|)^{2}-2|P{F}_{1}||P{F}_{2}|-$2|PF1||PF2|×cos60°,
∴4=16-3|PF1||PF2|,即|PF1||PF2|=4.
∴△F1PF2的面积S=$\frac{1}{2}$|PF1||PF2|sin60°=$\frac{1}{2}×4×\frac{\sqrt{3}}{2}=\sqrt{3}$.
点评 本题考查椭圆的简单性质,考查了椭圆定义及余弦定理在求解焦点三角形中的应用,是中档题.

练习册系列答案
相关题目
7.各项都是正数的等比数列{an}的公比q≠1,a3,a5,a6成等差数列,则$\frac{{{a_3}+{a_4}}}{{{a_4}+{a_5}}}$=( )
| A. | $\frac{{-1+\sqrt{3}}}{2}$ | B. | $\frac{{-1+\sqrt{5}}}{2}$ | C. | $\frac{{1+\sqrt{5}}}{2}$ | D. | $2+\sqrt{5}$ |
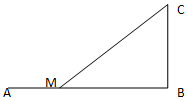 如图,设铁路AB长为50,BC⊥AB,且BC=10,为将货物从A运往C,现在AB上距点B为x的点M处修一公路至C,已知单位距离的铁路运费为2,公路运费为4.
如图,设铁路AB长为50,BC⊥AB,且BC=10,为将货物从A运往C,现在AB上距点B为x的点M处修一公路至C,已知单位距离的铁路运费为2,公路运费为4.