题目内容
9.已知实数x满足9x-4×3x+1+27≤0且f(x)=(log2$\frac{x}{2}$)(log${\;}_{\sqrt{2}}$$\frac{\sqrt{x}}{2}$).(Ⅰ)求实数x的取值范围;
(Ⅱ)求f(x)的最大值和最小值,并求此时x的值.
分析 (1)转化为二次不等式求解即可.
(2)根据对数的运算法则,化简f(x),转化为二次函数求解值域.
解答 解:(1)实数x满足9x-4×3x+1+27≤0,
化解可得:(3x)2-12•3x+27≤0,
即(3x-3)(3x-9)≤0,
得3≤3x≤9,
∴1≤x≤2,
故得x的取值范围为[1,2];
(2)f(x)=(log2$\frac{x}{2}$)(log${\;}_{\sqrt{2}}$$\frac{\sqrt{x}}{2}$).
化解可得:f(x)=(log2x-log22)($2lo{g}_{2}\frac{\sqrt{x}}{2}$)
=(log2x-log22)(log2x-log24)
=(log2x-1)(log2x-2)
=($lo{g}_{2}x-\frac{3}{2}$)2-$\frac{1}{4}$
∵x∈[1,2],
∴log2x∈[0,1],
∴0≤=($lo{g}_{2}x-\frac{3}{2}$)2-$\frac{1}{4}$≤2.
∴当x=2时,f(x)有最小值0,当x=1时,f(x)有最大值2.
点评 本题考查了指数的运算和对数的运算,转化思想,利用二次函数的配方求解最值问题.属于基础题

练习册系列答案
相关题目
20.已知平面区域Ω:$\left\{{\begin{array}{l}{3x+4y-18≤0}\\{x≥2}\\{y≥0}\end{array}}$,夹在两条斜率为-$\frac{3}{4}$的平行直线之间,且这两条平行直线间的最短距离为m.若点P(x,y)∈Ω,且mx-y的最小值为p,$\frac{y}{x+m}$的最大值为q,则pq等于( )
| A. | $\frac{27}{22}$ | B. | $\frac{2}{5}$ | C. | $\frac{27}{25}$ | D. | 0 |
17.已知函数f(x)为定义在R上的奇函数,且f(x)在[0,+∞)上单调递增,若f(a)<f(2a-1),则a的取值范围是( )
| A. | (-∞,1) | B. | (-∞,$\frac{1}{2}$) | C. | ($\frac{1}{2}$,1) | D. | (1,+∞) |
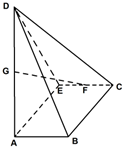 已知底面为矩形的四棱锥D-ABCE,AB=1,BC=2,AD=3,DE=$\sqrt{5}$,DE⊥AE,G、F分别为AD,CE的中点,其中二面角D-AE-C的平面角的正切值为-tan2.
已知底面为矩形的四棱锥D-ABCE,AB=1,BC=2,AD=3,DE=$\sqrt{5}$,DE⊥AE,G、F分别为AD,CE的中点,其中二面角D-AE-C的平面角的正切值为-tan2.