题目内容
10.函数f(x)=x3-ax在(1,3)上存在单调增区间,则a的取值范围是(-∞,27),函数f(x)=x3-ax在(1,3)上单调增,则a的取值范围是(-∞,3].分析 (1)问题转化为存在f′(x)=3x2-a>0在(1,3)成立,即存在a<3x2在(1,3)成立,即a<(3x2)max=27,从而求出a的范围即可;
(2)由函数f(x)=x3-ax在区间(1,3)上递增,可得:f'(x)=3x2-a≥0在(1,3)上恒成立,即a≤3x2在(1,3)上恒成立,结合二次函数的图象和性质,可得a的取值范围.
解答 解:(1)若函数f(x)=x3-ax在(1,3)上存在单调增区间,
则存在f′(x)=3x2-a>0在(1,3)成立,
即存在a<3x2在(1,3)成立,
即a<(3x2)max=27,
故a的范围是(-∞,27);
(2)函数f(x)=x3-ax在区间(1,3)上单调递增,
∴f'(x)=3x2-a≥0在(1,3)上恒成立,
∴a≤3x2在(1,3)上恒成立,
∴a≤3,
故a的取值范围是(-∞,3],
故答案为:(-∞,27),(-∞,3].
点评 本题考查了函数的单调性、最值问题,考查导数的应用,是一道中档题.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
20.已知平面区域Ω:$\left\{{\begin{array}{l}{3x+4y-18≤0}\\{x≥2}\\{y≥0}\end{array}}$,夹在两条斜率为-$\frac{3}{4}$的平行直线之间,且这两条平行直线间的最短距离为m.若点P(x,y)∈Ω,且mx-y的最小值为p,$\frac{y}{x+m}$的最大值为q,则pq等于( )
| A. | $\frac{27}{22}$ | B. | $\frac{2}{5}$ | C. | $\frac{27}{25}$ | D. | 0 |
1.已知椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1的左、右焦点分别为F1,F2,过F1的直线l交椭圆与两点A,B,则|AF2|+|BF2|的最大值为( )
| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
15.“$\frac{1}{x}<\frac{1}{2}$”是“x>2”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
20.已知集合P={1,3,5,7},Q={x|2x-1>11},则P∩Q等于( )
| A. | {7} | B. | {5,7} | C. | {3,5,7} | D. | {x|6<x≤7} |
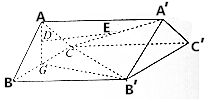 已知正三棱柱ABC-A′B′C′如图所示,其中G是BC的中点,D,E分别在线段AG,A′C上运动,使得DE∥平面BCC′B′,CC′=2BC=4.
已知正三棱柱ABC-A′B′C′如图所示,其中G是BC的中点,D,E分别在线段AG,A′C上运动,使得DE∥平面BCC′B′,CC′=2BC=4. 如图,矩形O′A′B′C′是水平放置的一个平面图形的直观图,其中O′A′=6,O′C′=2,则原图形OABC的面积为24$\sqrt{2}$.
如图,矩形O′A′B′C′是水平放置的一个平面图形的直观图,其中O′A′=6,O′C′=2,则原图形OABC的面积为24$\sqrt{2}$.