题目内容
11.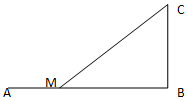 如图,设铁路AB长为50,BC⊥AB,且BC=10,为将货物从A运往C,现在AB上距点B为x的点M处修一公路至C,已知单位距离的铁路运费为2,公路运费为4.
如图,设铁路AB长为50,BC⊥AB,且BC=10,为将货物从A运往C,现在AB上距点B为x的点M处修一公路至C,已知单位距离的铁路运费为2,公路运费为4.(1)将总运费y表示为x的函数;
(2)如何选点M才使总运费最小?
分析 (1)由已知中铁路AB长为50,BC⊥AB,且BC=10,为将货物从A运往C,现在AB上距点B为x的点M处修一公路至C,已知单位距离的铁路运费为2,公路运费为4,我们可计算出公路上的运费和铁路上的运费,进而得到由A到C的总运费;
(2)由(1)中所得的总运费y表示为x的函数,利用导数法,我们可以分析出函数的单调性,及函数的最小值点,得到答案.
解答 解:(1)依题中,铁路AB长为50,BC⊥AB,且BC=10,
将货物从A运往C,现在AB上距点B为x的点M处修一公路至C,
且单位距离的铁路运费为2,公路运费为4
∴铁路AM上的运费为2(50-x),公路MC上的运费为4 $\sqrt{100{+x}^{2}}$,
则由A到C的总运费为y=2(50-x)+4 $\sqrt{100{+x}^{2}}$(0≤x≤50)…(6分)
(2)y′=-2+$\frac{4x}{\sqrt{100{+x}^{2}}}$(0≤x≤50),
令y′=0,
解得x=$\frac{10}{\sqrt{3}}$,或x=-$\frac{10}{\sqrt{3}}$(舍)…(9分)
当0≤x≤$\frac{10}{\sqrt{3}}$时,y′≤0;当$\frac{10}{\sqrt{3}}$≤x≤50时,y′≥0
故当x=$\frac{10}{\sqrt{3}}$时,y取得最小值.…(12分)
即当在距离点B为$\frac{10}{\sqrt{3}}$时的点M处修筑公路至C时总运费最省.…(13)
点评 本题考查的知识点是导数在最大值最小值问题中的应用,函数最值的应用,其中根据已知条件求出函数的解析式,并确定函数的单调性是解答本题的关键.

练习册系列答案
相关题目
1.已知椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1的左、右焦点分别为F1,F2,过F1的直线l交椭圆与两点A,B,则|AF2|+|BF2|的最大值为( )
| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
16.若实数x,y满足$\left\{\begin{array}{l}x+y≥3\\ x-y≤3\\ x+2y≤6\end{array}\right.$,则(x+1)2+y2的最小值为( )
| A. | $2\sqrt{2}$ | B. | $\sqrt{10}$ | C. | 8 | D. | 10 |
20.已知集合P={1,3,5,7},Q={x|2x-1>11},则P∩Q等于( )
| A. | {7} | B. | {5,7} | C. | {3,5,7} | D. | {x|6<x≤7} |
 如图,矩形O′A′B′C′是水平放置的一个平面图形的直观图,其中O′A′=6,O′C′=2,则原图形OABC的面积为24$\sqrt{2}$.
如图,矩形O′A′B′C′是水平放置的一个平面图形的直观图,其中O′A′=6,O′C′=2,则原图形OABC的面积为24$\sqrt{2}$.