题目内容
2.已知函数$f(x)=cosx•cos(x-\frac{π}{3})$.(1)求函数f(x)的单调增区间;
(2)若直线y=a与函数f(x)的图象无公共点,求实数a的取值范围.
分析 (1)运用两角差的余弦公式和二倍角公式,化简可得f(x),再由余弦函数的单调区间,解不等式可得所求增区间;
(2)求得f(x)的最值,即可得到a的取值范围.
解答 解:(1)函数$f(x)=cosx•cos(x-\frac{π}{3})$=cosx($\frac{1}{2}$cosx+$\frac{\sqrt{3}}{2}$sinx)
=$\frac{1+cos2x}{4}$+$\frac{\sqrt{3}}{4}$sin2x=$\frac{1}{2}$cos(2x-$\frac{π}{3}$)+$\frac{1}{4}$,
由2kπ-π≤2x-$\frac{π}{3}$≤2kπ,k∈Z,
解得kπ-$\frac{π}{3}$≤x≤kπ+$\frac{π}{6}$,k∈Z,
即f(x)的增区间为[kπ-$\frac{π}{3}$,kπ+$\frac{π}{6}$],k∈Z;
(2)由(1)可得当2x-$\frac{π}{3}$=2kπ,即x=kπ+$\frac{π}{6}$,k∈Z时,f(x)取得最大值$\frac{3}{4}$;
当2x-$\frac{π}{3}$=2kπ+π,即x=kπ+$\frac{2π}{3}$,k∈Z时,f(x)取得最小值-$\frac{1}{4}$.
由直线y=a与函数f(x)的图象无公共点,
可得a的范围是a>$\frac{3}{4}$或a<-$\frac{1}{4}$.
点评 本题考查三角函数的化简和求值,考查余弦函数的图象和性质,属于中档题.

练习册系列答案
相关题目
12.不等式组$\left\{\begin{array}{l}{x-y≥1}\\{x+3y≤3}\end{array}\right.$的解集记为D,有下面四个命题:
p1:?(x,y)∈D,2x-8y≥2; p2:?(x,y)∈D,2x-8y<2
p3:?(x,y)∈D,2x-8y≥-1 p4:?(x,y)∈D,2x-8y<-1
其中的真命题是( )
p1:?(x,y)∈D,2x-8y≥2; p2:?(x,y)∈D,2x-8y<2
p3:?(x,y)∈D,2x-8y≥-1 p4:?(x,y)∈D,2x-8y<-1
其中的真命题是( )
| A. | p2,p3 | B. | p1,p4 | C. | p1,p2 | D. | p1,p3 |
13.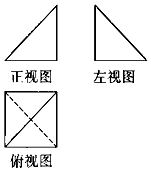 如图1,一个多面体的正视图和侧视图是两个全等的等腰直角三角形且直角边长为2,俯视图是边长为2的正方形,则该多面体的表面积是( )
如图1,一个多面体的正视图和侧视图是两个全等的等腰直角三角形且直角边长为2,俯视图是边长为2的正方形,则该多面体的表面积是( )
 如图1,一个多面体的正视图和侧视图是两个全等的等腰直角三角形且直角边长为2,俯视图是边长为2的正方形,则该多面体的表面积是( )
如图1,一个多面体的正视图和侧视图是两个全等的等腰直角三角形且直角边长为2,俯视图是边长为2的正方形,则该多面体的表面积是( )| A. | $2+4\sqrt{2}+2\sqrt{3}$ | B. | $2+4\sqrt{2}+\sqrt{6}$ | C. | $2+4\sqrt{2}$ | D. | $\frac{4}{3}$ |
10.函数$f(x)=sin(\frac{π}{2}-x)$是( )
| A. | 奇函数,且在区间$(0,\frac{π}{2})$上单调递增 | B. | 奇函数,且在区间$(0,\frac{π}{2})$上单调递减 | ||
| C. | 偶函数,且在区间$(0,\frac{π}{2})$上单调递增 | D. | 偶函数,且在区间$(0,\frac{π}{2})$上单调递减 |
14.已知函数f(x)=ln|ax|(a≠0),g(x)=x-3+sinx,则( )
| A. | f(x)+g(x)是偶函数 | B. | f(x)•g(x)是偶函数 | C. | f(x)+g(x)是奇函数 | D. | f(x)•g(x)是奇函数 |