题目内容
4.设函数$f(x)=\sqrt{x-1}$,则$f(\frac{x}{2})+f(\frac{4}{x})$的定义域为( )| A. | $[\frac{1}{2},4]$ | B. | [2,4] | C. | [1,+∞) | D. | [$\frac{1}{4}$,2] |
分析 求出函数f(x)的定义域,再进一步求出复合函数的定义域,即可得答案.
解答 解:∵函数$f(x)=\sqrt{x-1}$的定义域为:[1,+∞).
∴$\left\{\begin{array}{l}{\frac{x}{2}≥1}\\{\frac{4}{x}≥1}\end{array}\right.$,
解得2≤x≤4.
∴$f(\frac{x}{2})+f(\frac{4}{x})$的定义域为:[2,4].
故选:B.
点评 本题考查了函数的定义域及其求法,考查了不等式的解法,是基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.若集合A={-1,1},B={0,1},则集合A∪B的子集个数为( )
| A. | 4 | B. | 5 | C. | 7 | D. | 8 |
12.不等式组$\left\{\begin{array}{l}{x-y≥1}\\{x+3y≤3}\end{array}\right.$的解集记为D,有下面四个命题:
p1:?(x,y)∈D,2x-8y≥2; p2:?(x,y)∈D,2x-8y<2
p3:?(x,y)∈D,2x-8y≥-1 p4:?(x,y)∈D,2x-8y<-1
其中的真命题是( )
p1:?(x,y)∈D,2x-8y≥2; p2:?(x,y)∈D,2x-8y<2
p3:?(x,y)∈D,2x-8y≥-1 p4:?(x,y)∈D,2x-8y<-1
其中的真命题是( )
| A. | p2,p3 | B. | p1,p4 | C. | p1,p2 | D. | p1,p3 |
9.已知正数a,b,c满足4a-2b+25c=0,则lga+lgc-2lgb的最大值为( )
| A. | -2 | B. | 2 | C. | -1 | D. | 1 |
13.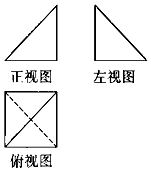 如图1,一个多面体的正视图和侧视图是两个全等的等腰直角三角形且直角边长为2,俯视图是边长为2的正方形,则该多面体的表面积是( )
如图1,一个多面体的正视图和侧视图是两个全等的等腰直角三角形且直角边长为2,俯视图是边长为2的正方形,则该多面体的表面积是( )
 如图1,一个多面体的正视图和侧视图是两个全等的等腰直角三角形且直角边长为2,俯视图是边长为2的正方形,则该多面体的表面积是( )
如图1,一个多面体的正视图和侧视图是两个全等的等腰直角三角形且直角边长为2,俯视图是边长为2的正方形,则该多面体的表面积是( )| A. | $2+4\sqrt{2}+2\sqrt{3}$ | B. | $2+4\sqrt{2}+\sqrt{6}$ | C. | $2+4\sqrt{2}$ | D. | $\frac{4}{3}$ |
14.已知函数f(x)=ln|ax|(a≠0),g(x)=x-3+sinx,则( )
| A. | f(x)+g(x)是偶函数 | B. | f(x)•g(x)是偶函数 | C. | f(x)+g(x)是奇函数 | D. | f(x)•g(x)是奇函数 |
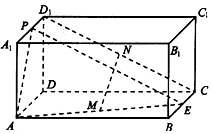 如图,在长方体ABCD-A1B1C1D1中,E、P分别是BC、A1D1的中点.M、N分别是AE、CD1的中点,AD=AA1=$\frac{1}{2}$AB=2.
如图,在长方体ABCD-A1B1C1D1中,E、P分别是BC、A1D1的中点.M、N分别是AE、CD1的中点,AD=AA1=$\frac{1}{2}$AB=2.