��Ŀ����
3����ֱ֪��m��n��ƽ���������������ȷ���ǣ�������| A�� | $\left.{\begin{array}{l}{m��n}\\{n?��}\end{array}}\right\}⇒m�ͦ�$ | B�� | $\left.{\begin{array}{l}{m��n}\\{n�ͦ�}\end{array}}\right\}⇒m�Φ�$ | C�� | $\left.{\begin{array}{l}{m�ͦ�}\\{n�Φ�}\end{array}}\right\}⇒m��n$ | D�� | $\left.{\begin{array}{l}{m�Φ�}\\{n?��}\end{array}}\right\}⇒m��n$ |
���� A��ֱ��m��ֱƽ�����һ��ֱ�ߣ����ܵõ�ֱ��m��ֱƽ�����
B��m��n��n�ͦ�⇒m�Φ���m?����
C��m�ͦ�⇒m��ֱ���ڼ����ƽ�е�����ֱ�ߣ�
D����m�Φ���n?����⇒m��n��m��n���森
��� �⣺����A��ֱ��m��ֱƽ�����һ��ֱ�ߣ����ܵõ�ֱ��m��ֱƽ������ʴ���
����B��m��n��n�ͦ�⇒m�Φ���m?�����ʴ���
����C��m�ͦ�⇒m��ֱ���ڼ����ƽ�е�����ֱ�ߣ�����ȷ��
����D����m�Φ���n?����⇒m��n��m��n���棬�ʴ���
��ѡ��C��
���� ���⿼���˿ռ����ߡ�����λ�ù�ϵ�����ڻ����⣮

��ϰ��ϵ�д�
 ��ĩ���100�ִ��½����ȫ�Ծ�ϵ�д�
��ĩ���100�ִ��½����ȫ�Ծ�ϵ�д�
�����Ŀ
13����ȱ�����{an}�Ĺ���q=1��ǰn���ΪSn����$\frac{{S}_{4}}{{a}_{2}}$=��������
| A�� | 2 | B�� | 4 | C�� | $\frac{15}{2}$ | D�� | $\frac{17}{2}$ |
15��������A={-1��1}��B={0��1}����A��B���Ӽ�����Ϊ��������
| A�� | 4 | B�� | 5 | C�� | 7 | D�� | 8 |
12������ʽ��$\left\{\begin{array}{l}{x-y��1}\\{x+3y��3}\end{array}\right.$�Ľ⼯��ΪD���������ĸ����⣺
p1��?��x��y����D��2x-8y��2�� p2��?��x��y����D��2x-8y��2
p3��?��x��y����D��2x-8y��-1 p4��?��x��y����D��2x-8y��-1
���е��������ǣ�������
p1��?��x��y����D��2x-8y��2�� p2��?��x��y����D��2x-8y��2
p3��?��x��y����D��2x-8y��-1 p4��?��x��y����D��2x-8y��-1
���е��������ǣ�������
| A�� | p2��p3 | B�� | p1��p4 | C�� | p1��p2 | D�� | p1��p3 |
13��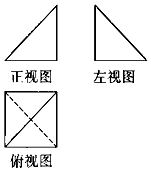 ��ͼ1��һ�������������ͼ�Ͳ���ͼ������ȫ�ȵĵ���ֱ����������ֱ�DZ߳�Ϊ2������ͼ�DZ߳�Ϊ2�������Σ���ö�����ı�����ǣ�������
��ͼ1��һ�������������ͼ�Ͳ���ͼ������ȫ�ȵĵ���ֱ����������ֱ�DZ߳�Ϊ2������ͼ�DZ߳�Ϊ2�������Σ���ö�����ı�����ǣ�������
 ��ͼ1��һ�������������ͼ�Ͳ���ͼ������ȫ�ȵĵ���ֱ����������ֱ�DZ߳�Ϊ2������ͼ�DZ߳�Ϊ2�������Σ���ö�����ı�����ǣ�������
��ͼ1��һ�������������ͼ�Ͳ���ͼ������ȫ�ȵĵ���ֱ����������ֱ�DZ߳�Ϊ2������ͼ�DZ߳�Ϊ2�������Σ���ö�����ı�����ǣ�������| A�� | $2+4\sqrt{2}+2\sqrt{3}$ | B�� | $2+4\sqrt{2}+\sqrt{6}$ | C�� | $2+4\sqrt{2}$ | D�� | $\frac{4}{3}$ |
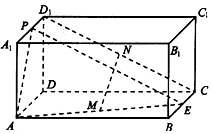 ��ͼ���ڳ�����ABCD-A1B1C1D1�У�E��P�ֱ���BC��A1D1���е㣮M��N�ֱ���AE��CD1���е㣬AD=AA1=$\frac{1}{2}$AB=2��
��ͼ���ڳ�����ABCD-A1B1C1D1�У�E��P�ֱ���BC��A1D1���е㣮M��N�ֱ���AE��CD1���е㣬AD=AA1=$\frac{1}{2}$AB=2��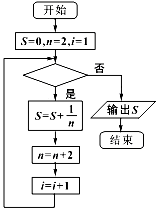
 ��ͼ���ı���ABCD��ƽ���ı��Σ�ƽ��AED��ƽ��ABCD��EF��AB��$BC=EF=\frac{1}{2}AB$����BAD=60�㣬GΪBC���е㣮
��ͼ���ı���ABCD��ƽ���ı��Σ�ƽ��AED��ƽ��ABCD��EF��AB��$BC=EF=\frac{1}{2}AB$����BAD=60�㣬GΪBC���е㣮