题目内容
在△ABC中，角A，B，C（C为钝角）所对的边分别为a，b，c，且cos（A+B-C）=
，a=2，
=2．
（1）求cosC的值；
（2）求b的长．
| 1 |
| 4 |
| sin(A+B) |
| sinA |
（1）求cosC的值；
（2）求b的长．
考点：余弦定理,正弦定理
专题：解三角形
分析：（1）已知第二个等式利用正弦定理化简，把a的值代入求出c的值，第一个等式中的角度变形后，利用诱导公式及二倍角的余弦函数公式化简，即可求出cosC的值；
（2）利用余弦定理列出关系式，把a，c，cosC的值代入即可求出b的值．
（2）利用余弦定理列出关系式，把a，c，cosC的值代入即可求出b的值．
解答：
解：（1）由正弦定理得：
=
=
=2，即c=2a=4，
∵cos（A+B-C）=cos（π-2C）=-cos2C=-2cos2C+1=
，
∴cosC=-
；
（2）由余弦定理得：cosC=
，
把a=2，c=4，cosC=-
代入得：b=2
．
| c |
| a |
| sinC |
| sinA |
| sin(A+B) |
| sinA |
∵cos（A+B-C）=cos（π-2C）=-cos2C=-2cos2C+1=
| 1 |
| 4 |
∴cosC=-
| ||
| 4 |
（2）由余弦定理得：cosC=
| a2+b2-c2 |
| 2ab |
把a=2，c=4，cosC=-
| ||
| 4 |
| 6 |
点评：此题考查了正弦、余弦定理，以及诱导公式，熟练掌握定理是解本题的关键．
练习册系列答案
相关题目
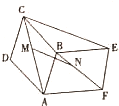如图所示，ABCD-ABEF都是平行四边形，且不共面，M、N分别是AC、BF的中点，判断
已知函数f（x）=Asin（ωx+Φ）（A＞0，ω＞0，|Φ|＜π）的部分图象如图所示．两位老师和两位同学站成一排合影，则两位老师至少有一人站在两端的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|