题目内容
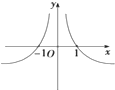
 已知函数f(x)=Asin(ωx+Φ)(A>0,ω>0,|Φ|<π)的部分图象如图所示.
已知函数f(x)=Asin(ωx+Φ)(A>0,ω>0,|Φ|<π)的部分图象如图所示.(Ⅰ)求函数f(x)的解析式;
(Ⅱ)求函数f(x)在区间[-
| π |
| 6 |
| π |
| 4 |
考点:由y=Asin(ωx+φ)的部分图象确定其解析式
专题:三角函数的图像与性质
分析:(Ⅰ)根据已知和图象,先求出A,ω的值,再求出φ的值,即可确定函数f(x)的解析式;
(Ⅱ)先确定2x+
∈[-
,
],则可确定得-1≤2sin(2x+
)≤2,
(Ⅱ)先确定2x+
| π |
| 6 |
| π |
| 6 |
| 2π |
| 3 |
| π |
| 6 |
解答:
解:(Ⅰ)依题意,A=2
且
=-
-(-
)=
,得T=π=
,所以ω=2,
且f(0)=1,得2sinφ=
,|φ|<π,且点(0,1)在函数f(x)的递增区间上,故-
<φ<
,因此φ=
,
所以f(x)=2sin(2x+
)
(Ⅱ)当x∈[-
,
]时,2x+
∈[-
,
]
得-1≤2sin(2x+
)≤2
当2x+
=-
时,即有x=-
时,函数f(x)取得最小值-1;
当2x+
=
时,即有x=
时,函数f(x)取得最大小值2.
且
| T |
| 4 |
| π |
| 3 |
| 7π |
| 12 |
| π |
| 4 |
| 2π |
| ω |
且f(0)=1,得2sinφ=
| 1 |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 6 |
所以f(x)=2sin(2x+
| π |
| 6 |
(Ⅱ)当x∈[-
| π |
| 6 |
| π |
| 4 |
| π |
| 6 |
| π |
| 6 |
| 2π |
| 3 |
得-1≤2sin(2x+
| π |
| 6 |
当2x+
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
当2x+
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
点评:本题主要考察了由y=Asin(ωx+φ)的部分图象确定其解析式,三角函数的图象与性质,属于中档题.

练习册系列答案
相关题目
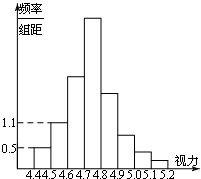 为了解某校高三学生的视力情况,随机地抽查了该校100名高三学生的视力情况,得到频率分布直方图,由于不慎将部分数据丢失,但知道后5组的频数成等比数列,设视力在4.6到4.9之间的学生数为a,最大频率为b,则a,b的值分别为( )
为了解某校高三学生的视力情况,随机地抽查了该校100名高三学生的视力情况,得到频率分布直方图,由于不慎将部分数据丢失,但知道后5组的频数成等比数列,设视力在4.6到4.9之间的学生数为a,最大频率为b,则a,b的值分别为( )| A、77,0.53 |
| B、70,0.32 |
| C、77,5.3 |
| D、70,3.2 |