题目内容
设f(x)是R上的奇函数,且对任意的实数a,b,当a+b≠0时,都有
>0.
(1)若a>b,试比较f(a),f(b)的大小;
(2)若存在实数x∈[
,
],使得不等式f(x-c2)>0成立,试求实数c的取值范围.
| f(a)+f(b) |
| a+b |
(1)若a>b,试比较f(a),f(b)的大小;
(2)若存在实数x∈[
| 1 |
| 2 |
| 3 |
| 2 |
考点:奇偶性与单调性的综合
专题:函数的性质及应用
分析:(1)先根据单调性的定义判断f(x)在R上的单调性:设x1<x2,根据已知条件便可得到
=
>0,从而得到f(x1)<f(x2),所以函数f(x)在R上单调递增,所以若a>b,便有f(a)>f(b);
(2)因为f(x)是R上的奇函数,所以f(0)=0,所以原不等式等价于f(x-c2)>f(0),根据f(x)的单调性便得x-c2>0,所以c2<x,因为x∈[
,
],所以c2<
,解该不等式即得c的取值范围.
| f(x1)-f(x2) |
| x1-x2 |
| f(x1)+f(-x2) |
| x1+(-x2) |
(2)因为f(x)是R上的奇函数,所以f(0)=0,所以原不等式等价于f(x-c2)>f(0),根据f(x)的单调性便得x-c2>0,所以c2<x,因为x∈[
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
解答:
解:(1)设x1,x2∈R,且x1<x2,则根据已知条件有:
=
>0;
∵x1-x2<0,∴f(x1)<f(x2);
∴f(x)在R上是增函数;
∵a>b,∴f(a)>f(b);
(2)f(0)=0,f(x)在R上是增函数;
∴由f(x-c2)>0得f(x-c2)>f(0);
∴x-c2>0,即c2<x;
∴c2<
,-
<c<
;
∴实数c的取值范围是(-
,
).
| f(x1)-f(x2) |
| x1-x2 |
| f(x1)+f(-x2) |
| x1+(-x2) |
∵x1-x2<0,∴f(x1)<f(x2);
∴f(x)在R上是增函数;
∵a>b,∴f(a)>f(b);
(2)f(0)=0,f(x)在R上是增函数;
∴由f(x-c2)>0得f(x-c2)>f(0);
∴x-c2>0,即c2<x;
∴c2<
| 3 |
| 2 |
| ||
| 2 |
| ||
| 2 |
∴实数c的取值范围是(-
| ||
| 2 |
| ||
| 2 |
点评:考查函数单调性的定义,以及根据定义证明函数的单调性,f(x)在R上是奇函数时f(0)=0.

练习册系列答案
相关题目
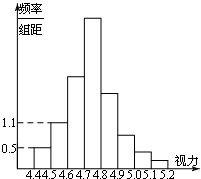 为了解某校高三学生的视力情况,随机地抽查了该校100名高三学生的视力情况,得到频率分布直方图,由于不慎将部分数据丢失,但知道后5组的频数成等比数列,设视力在4.6到4.9之间的学生数为a,最大频率为b,则a,b的值分别为( )
为了解某校高三学生的视力情况,随机地抽查了该校100名高三学生的视力情况,得到频率分布直方图,由于不慎将部分数据丢失,但知道后5组的频数成等比数列,设视力在4.6到4.9之间的学生数为a,最大频率为b,则a,b的值分别为( )| A、77,0.53 |
| B、70,0.32 |
| C、77,5.3 |
| D、70,3.2 |
(文做)函数f(x)=(x-1)(x-2)+(x-2)(x-3)+(x-3)(x-1)的两个零点分别位于区间( )
| A、(2,3)和(3,+∞)内 |
| B、(-∞,1)和(1,2)内 |
| C、(1,2)和(2,3)内 |
| D、(-∞,1)和(3,+∞)内 |
下列有关命题的说法正确的是( )
| A、命题“若x2=1,则x=1”的否命题为“若x2=1,则x≠1” |
| B、“x=-1”是“x2-2x-3=0”的必要不充分条件 |
| C、命题“?x∈R使得x2+x-1<0”的否定是“?x∈R,均有x2+x-1>0” |
| D、命题“已知x,y∈R,若x+y≠5,则x≠1或y≠4”为真命题 |