题目内容
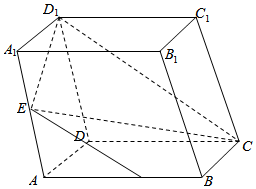
16.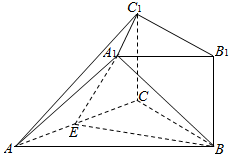 在如图所示的几何体中,四边形BB1C1C是矩形,BB1⊥平面ABC,A1B1∥AB,AB=2A1B1,E是AC的中点.
在如图所示的几何体中,四边形BB1C1C是矩形,BB1⊥平面ABC,A1B1∥AB,AB=2A1B1,E是AC的中点.(1)求证:A1E∥平面BB1C1C;
(2)若AC=BC,AB=2BB1,求证:平面BEA1⊥平面AA1C1.
分析 (1)取AB的中点F,连结EF,A1F.则可通过证明平面A1EF∥平面BB1C1C得出A1E∥平面BB1C1C;
(2)连结CF,则可得出CF∥A1C1,通过证明CF⊥平面平面ABB1A1得到CF⊥A1B.即A1C1⊥A1B,利用勾股定理的逆定理得出AA1⊥A1B,于是A1B⊥平面AA1C1,从而平面BEA1⊥平面AA1C1.
解答  证明:(1)取AB的中点F,连结EF,A1F
证明:(1)取AB的中点F,连结EF,A1F
∵AB=2A1B1,∴BF=A1B1,
又A1B1∥AB,∴四边形A1FBB1是平行四边形,
∴A1F∥BB1,
∵E,F分别AC,AB的中点,
∴EF∥BC,
又EF?平面A1EF,A1F?平面A1EF,EF∩A1F=F,BC?平面BB1C1C,BB1?平面BB1C1C,BC∩BB1=B,
∴平面A1EF∥平面BB1C1C.
又A1E?平面A1EF,
∴A1E∥平面BB1C1C.
(2)连结CF,
∵BB1⊥平面ABC,∴BB1⊥BF,BB1⊥CF,
∵AC=BC,F是AB的中点,∴CF⊥AB,
又AB?平面ABB1A1,BB1?平面ABB1A1,AB∩BB1=B,
∴CF⊥平面ABB1A1,又A1B?平面ABB1A1,
∴CF⊥A1B.
∴四边形A1FBB1是矩形,又四边形BB1C1C是矩形,
∴A1F$\stackrel{∥}{=}$BB1$\stackrel{∥}{=}$CC1,
∴四边形A1FCC1是平行四边形,∴A1C1∥CF.
∴A1C1⊥A1B.
∵AB=2A1B1=2BB1,
∴AF=BF=A1F,又AF1⊥AB,
∴△ABA1是等腰直角三角形,即AA1⊥A1B,
又AA1?平面AA1C1,A1C1?平面AA1C1,AA1∩A1C=A1,
∴A1B⊥平面AA1C1,又A1B?平面BEA1,
∴平面BEA1⊥平面AA1C1.
点评 本题考查了线面平行,面面垂直的判定,线面垂直的性质,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | 18 | B. | 24 | C. | 36 | D. | 48 |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
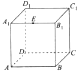 如图,正方体ABCD-A1B1C1D1的棱长为1,E为A1B1的中点,则下列五个命题:
如图,正方体ABCD-A1B1C1D1的棱长为1,E为A1B1的中点,则下列五个命题: