题目内容
11.设向量$\overrightarrow a$=(1,x),$\overrightarrow b$=(x,4),则“x=$\int_{1}^{e}{\frac{2}{t}}$dt”(e=2.718…是自然对数的底数)是“$\overrightarrow a$∥$\overrightarrow b$”的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 利用定积分求解x的值,然后判断充要条件即可.
解答 解:x=$\int_{1}^{e}{\frac{2}{t}}$dt=2lnx${|}_{1}^{e}$=2.
向量$\overrightarrow a$=(1,x)=(1,2),$\overrightarrow b$=(x,4)=(2,4),
可得“$\overrightarrow a$∥$\overrightarrow b$”,
但是“$\overrightarrow a$∥$\overrightarrow b$”,可得x=-2,
所以“x=$\int_{1}^{e}{\frac{2}{t}}$dt”(e=2.718…是自然对数的底数)是“$\overrightarrow a$∥$\overrightarrow b$”的充分不必要条件.
故选:A.
点评 本题考查充要条件的应用,定积分的求法,考查计算能力.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
2.若2sin2α=1-cos2α,则tanα等于( )
| A. | -2 | B. | 2 | C. | -2或0 | D. | 2或0 |
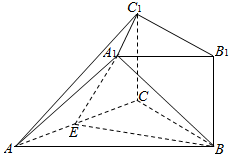 在如图所示的几何体中,四边形BB1C1C是矩形,BB1⊥平面ABC,A1B1∥AB,AB=2A1B1,E是AC的中点.
在如图所示的几何体中,四边形BB1C1C是矩形,BB1⊥平面ABC,A1B1∥AB,AB=2A1B1,E是AC的中点. 中国传统文化中很多内容体现了数学的对称美,如图所示的太极图是由黑白两个鱼形纹组成的圆形图案,充分展现了相互转化、对称统一的形式美、和谐美.给出定义:能够将圆O的周长和面积同时平分的函数称为这个圆的“优美函数”.给出下列命题:
中国传统文化中很多内容体现了数学的对称美,如图所示的太极图是由黑白两个鱼形纹组成的圆形图案,充分展现了相互转化、对称统一的形式美、和谐美.给出定义:能够将圆O的周长和面积同时平分的函数称为这个圆的“优美函数”.给出下列命题: