题目内容
6.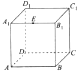 如图,正方体ABCD-A1B1C1D1的棱长为1,E为A1B1的中点,则下列五个命题:
如图,正方体ABCD-A1B1C1D1的棱长为1,E为A1B1的中点,则下列五个命题:①点E到平面ABC1D1的距离为$\frac{1}{2}$;
②直线BC与平面ABC1D1所成角为45°;
③空间四边形ABCD1在正方体六个面内的射影围成的图形中,面积最小的值为$\frac{1}{2}$;
④BE与CD1所成角的正弦值为$\frac{{\sqrt{10}}}{10}$;
⑤二面角A-BD1-C的大小为$\frac{5π}{6}$.
其中真命题是②③④.(写出所有真命题的序号)
分析 对5个命题分别进行判断,即可得出结论.
解答  解:①由于A1B1∥平面ABC1D1,故B1到平面ABC1D1的距离即点E到平面ABC1D1的距离,
解:①由于A1B1∥平面ABC1D1,故B1到平面ABC1D1的距离即点E到平面ABC1D1的距离,
连接B1C交BC1于F,则易得B1F垂直于平面ABC1D1,而B1F=$\frac{\sqrt{2}}{2}$,故点E到平面ABC1D1的距离为$\frac{\sqrt{2}}{2}$,故①错;
②易得B1C垂直于平面ABC1D1,故∠CBC1为直线BC与平面ABC1D1所成的角,且为45°,故②正确;
③易得空间四边形ABCD1在正方体的面ABCD、面A1B1C1D1内的射影面积为1,在面BB1C1C内、面AA1D1D内的射影面积为$\frac{1}{2}$,在面ABB1A1内、面CC1D1D内的射影面积为$\frac{1}{2}$,故③正确;
④BE与CD1所成的角,即为BA1与BE所成角,即为∠A1BE,A1E=$\frac{1}{2}$,BE=$\frac{\sqrt{5}}{2}$,BA1=$\sqrt{2}$,cos∠A1BE=$\frac{\frac{5}{4}+2-\frac{1}{4}}{2×\frac{\sqrt{5}}{2}×\sqrt{2}}$=$\frac{3\sqrt{10}}{10}$,sin∠A1BE=$\frac{\sqrt{10}}{10}$,故④正确;
⑤在直角三角形BAD1中过A作AH垂直于BD1,连接CH,易知CH垂直于BD1,故∠AHC是二面角A-BD1-C的平面角,由余弦定理得,cos∠AHC=$\frac{\frac{2}{3}+\frac{2}{3}-2}{2×\frac{\sqrt{6}}{3}×\frac{\sqrt{6}}{3}}$=-$\frac{1}{2}$,故∠AHC=$\frac{2π}{3}$,故⑤错.
故答案为:②③④
点评 本题考查命题的真假判断,考查空间线面位置关系,考查空间角,考查学生分析解决问题的能力,知识综合性强.

 阅读快车系列答案
阅读快车系列答案| A. | C${\;}_{8}^{3}$ | B. | ${C}_{8}^{4}$ | C. | ${C}_{8}^{5}$ | D. | ${C}_{8}^{6}$ |
| A. | (-2,-1) | B. | (-2,+∞) | C. | (-∞,-1) | D. | (-∞,-2)∪(-1,+∞) |
| A. | y=$\frac{1}{x}$ | B. | y=e-x | C. | y=-x3 | D. | y=lnx |
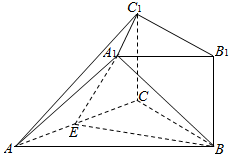 在如图所示的几何体中,四边形BB1C1C是矩形,BB1⊥平面ABC,A1B1∥AB,AB=2A1B1,E是AC的中点.
在如图所示的几何体中,四边形BB1C1C是矩形,BB1⊥平面ABC,A1B1∥AB,AB=2A1B1,E是AC的中点.