题目内容
已知函数f(x)的定义域为(-∞,-1)∪(1,+∞),对定义域内的任意x,满足f(x)+f(-x)=0,当x<-1时,f(x)=
(a为常),且x=2是函数f(x)的一个极值点,
(Ⅰ)求实数a的值;
(Ⅱ)如果当x≥2时,不等式f(x)≥
恒成立,求实数m的最大值;
(Ⅲ)求证:n-2(
+
+
+…+
)<ln(n+1).
| 1+ln(-x-1) |
| x+a |
(Ⅰ)求实数a的值;
(Ⅱ)如果当x≥2时,不等式f(x)≥
| m |
| x |
(Ⅲ)求证:n-2(
| 1 |
| 2 |
| 2 |
| 3 |
| 3 |
| 4 |
| n |
| n+1 |
考点:导数在最大值、最小值问题中的应用
专题:综合题,导数的综合应用
分析:(Ⅰ)先求出当x>1时,f(x)=-f(-x)=
,可得当x>1时,f′(x)=
,利用x=2是函数f(x)的一个极值点,即可求实数a的值;
(Ⅱ)当x≥2时,不等式f(x)≥
恒成立,等价于m≤x•
,令g(x)=x•
=1+
,求出最小值,即可求实数m的最大值;
(Ⅲ)由(Ⅱ)知,当x≥2时,f(x)≥
,即
≥
,可得ln(x-1)≥1-
>1-
,令x-1=
,则1-
=1-
,进而取值累加,即可证明结论.
| 1+ln(x-1) |
| x-a |
| ||
| (x-a)2 |
(Ⅱ)当x≥2时,不等式f(x)≥
| m |
| x |
| 1+ln(x-1) |
| x-1 |
| 1+ln(x-1) |
| x-1 |
| 1+xln(x-1) |
| x-1 |
(Ⅲ)由(Ⅱ)知,当x≥2时,f(x)≥
| 2 |
| x |
| 1+ln(x-1) |
| x-1 |
| 2 |
| x |
| 2 |
| x |
| 2 |
| x-1 |
| k+1 |
| k |
| 2 |
| x-1 |
| 2k |
| k+1 |
解答:
(Ⅰ)解:∵函数f(x)的定义域为(-∞,-1)∪(1,+∞),对定义域内的任意x,满足f(x)+f(-x)=0,
∴f(x)为奇函数,
当x>1时,-x<-1,∴f(x)=-f(-x)=
,
∴当x>1时,f′(x)=
∵x=2是函数f(x)的一个极值点,
∴f′(2)=
=0,
∴a=1;
(Ⅱ)解:由(Ⅰ)知,当x>1时,f(x)=
当x≥2时,不等式f(x)≥
恒成立,等价于m≤x•
,
令g(x)=x•
=1+
,
则g′(x)=
,
令h(x)=(x-1)-ln(x-1)(x≥2),则h′(x)=
,
当x>2时,h′(x)=
>0,函数h(x)在[2,+∞)上单调递增,
∴h(x)≥h(2)=1>0,
∴当x≥2时,g′(x)=
>0,
∴g(x)在[2,+∞)上单调递增,
∴g(x)min=g(2)=2,
∴m≤2,
∴实数m的最大值为2;
(Ⅲ)证明:由(Ⅱ)知,当x≥2时,f(x)≥
,即
≥
,
则ln(x-1)≥1-
>1-
,
令x-1=
,则1-
=1-
,
∴1-
<ln
;1-
<ln
,…,1-
<ln
,
累加可得n-2(
+
+
+…+
)<ln(n+1).
∴f(x)为奇函数,
当x>1时,-x<-1,∴f(x)=-f(-x)=
| 1+ln(x-1) |
| x-a |
∴当x>1时,f′(x)=
| ||
| (x-a)2 |
∵x=2是函数f(x)的一个极值点,
∴f′(2)=
| 1-a |
| (2-a)2 |
∴a=1;
(Ⅱ)解:由(Ⅰ)知,当x>1时,f(x)=
| 1+ln(x-1) |
| x-1 |
当x≥2时,不等式f(x)≥
| m |
| x |
| 1+ln(x-1) |
| x-1 |
令g(x)=x•
| 1+ln(x-1) |
| x-1 |
| 1+xln(x-1) |
| x-1 |
则g′(x)=
| (x-1)-ln(x-1) |
| (x-1)2 |
令h(x)=(x-1)-ln(x-1)(x≥2),则h′(x)=
| x-2 |
| x-1 |
当x>2时,h′(x)=
| x-2 |
| x-1 |
∴h(x)≥h(2)=1>0,
∴当x≥2时,g′(x)=
| (x-1)-ln(x-1) |
| (x-1)2 |
∴g(x)在[2,+∞)上单调递增,
∴g(x)min=g(2)=2,
∴m≤2,
∴实数m的最大值为2;
(Ⅲ)证明:由(Ⅱ)知,当x≥2时,f(x)≥
| 2 |
| x |
| 1+ln(x-1) |
| x-1 |
| 2 |
| x |
则ln(x-1)≥1-
| 2 |
| x |
| 2 |
| x-1 |
令x-1=
| k+1 |
| k |
| 2 |
| x-1 |
| 2k |
| k+1 |
∴1-
| 2×1 |
| 1+1 |
| 2 |
| 1 |
| 2×2 |
| 2+1 |
| 3 |
| 2 |
| 2n |
| n+1 |
| n+1 |
| n |
累加可得n-2(
| 1 |
| 2 |
| 2 |
| 3 |
| 3 |
| 4 |
| n |
| n+1 |
点评:本题考查导数知识的综合运用,考查函数的极值,考查恒成立问题,考查不等式的证明,正确分离参数求最值是关键.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
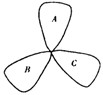 荷花池中,有一只青蛙在成品字形的三片荷叶上跳来跳去(每次跳跃时,均从一叶跳到另一叶),而且逆时针方向跳的概率是顺时针方向跳的概率的两倍,如图.假设现在青蛙在A叶上,则跳三次之后停在A叶上的概率是( )
荷花池中,有一只青蛙在成品字形的三片荷叶上跳来跳去(每次跳跃时,均从一叶跳到另一叶),而且逆时针方向跳的概率是顺时针方向跳的概率的两倍,如图.假设现在青蛙在A叶上,则跳三次之后停在A叶上的概率是( )