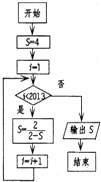
题目内容
已知向量
=(m,n),
=(cosx,sinx),函数f(x)=
•
-2.
(1)设m=n=1,x为某三角形的内角,求f(x)=-1时x的值;
(2)设m=4,n=3,当函数f(x)取最大值时,求cos2x的值.
| a |
| b |
| a |
| b |
(1)设m=n=1,x为某三角形的内角,求f(x)=-1时x的值;
(2)设m=4,n=3,当函数f(x)取最大值时,求cos2x的值.
考点:平面向量数量积的运算
专题:平面向量及应用
分析:(1)由题可知,当m=n=1时,f(x)=
•
-2=sinx+cosx-2,由f(x)=-1,求得sin(x+
)=
.结合x为三角形的内角,求得x的值;
(2)当m=4,n=3时,f(x)=5sin(x+φ)-2,当且仅当sin(x+φ)=1时,函数f(x)max=3.由此求得x的值,从而求得cos2x的值.
| a |
| b |
| π |
| 4 |
| ||
| 2 |
(2)当m=4,n=3时,f(x)=5sin(x+φ)-2,当且仅当sin(x+φ)=1时,函数f(x)max=3.由此求得x的值,从而求得cos2x的值.
解答:
解:(1)由题可知,f(x)=nsinx+mcosx-2,当m=n=1时,f(x)=
•
-2=sinx+cosx-2,
∵f(x)=-1⇒sinx+cosx=1⇒
sin(x+
)=1,
∴sin(x+
)=
.
∵x为三角形的内角,
∴x+
=
⇒x=
.
(2)当m=4,n=3时,f(x)=3sinx+4cosx-2=5sin(x+φ)-2,其中φ为锐角,且cosφ=
,sinφ=
,
当且仅当sin(x+φ)=1时,函数f(x)max=3.此时x+φ=2kπ+
(k∈Z)⇒x=2kπ+
-φ(k∈Z),
∴cosx=cos(2kπ+
-φ)=sinφ=
,
∴cos2x=2cos2x-1=2sin2φ-1=
.
| a |
| b |
∵f(x)=-1⇒sinx+cosx=1⇒
| 2 |
| π |
| 4 |
∴sin(x+
| π |
| 4 |
| ||
| 2 |
∵x为三角形的内角,
∴x+
| π |
| 4 |
| 3π |
| 4 |
| π |
| 2 |
(2)当m=4,n=3时,f(x)=3sinx+4cosx-2=5sin(x+φ)-2,其中φ为锐角,且cosφ=
| 3 |
| 5 |
| 4 |
| 5 |
当且仅当sin(x+φ)=1时,函数f(x)max=3.此时x+φ=2kπ+
| π |
| 2 |
| π |
| 2 |
∴cosx=cos(2kπ+
| π |
| 2 |
| 4 |
| 5 |
∴cos2x=2cos2x-1=2sin2φ-1=
| 7 |
| 25 |
点评:本题主要考查两个向量的数量积公式,三角函数的恒等变换,属于中档题.

练习册系列答案
相关题目
在△ABC中,角A,B,C的对边分别a,b,c,若a2+b2=
c2.则直线ax-by+c=0被圆x2+y2=9所截得的弦长为( )
| 1 |
| 2 |
A、2
| ||
B、3
| ||
C、2
| ||
D、3
|
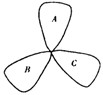 荷花池中,有一只青蛙在成品字形的三片荷叶上跳来跳去(每次跳跃时,均从一叶跳到另一叶),而且逆时针方向跳的概率是顺时针方向跳的概率的两倍,如图.假设现在青蛙在A叶上,则跳三次之后停在A叶上的概率是( )
荷花池中,有一只青蛙在成品字形的三片荷叶上跳来跳去(每次跳跃时,均从一叶跳到另一叶),而且逆时针方向跳的概率是顺时针方向跳的概率的两倍,如图.假设现在青蛙在A叶上,则跳三次之后停在A叶上的概率是( )A、
| ||
B、
| ||
C、
| ||
D、
|
设z=
+(1-i)2,则(1+x)4(1+zx)3展开式中x5项的系数是( )
| 1+i |
| 1-i |
| A、-2-3i |
| B、-12+3i |
| C、1+21i |
| D、-35i |