题目内容
若不等式|x+1|-|x-2|≤a对于任意实数x恒成立,则实数a的取值范围是 .
考点:绝对值不等式的解法
专题:不等式的解法及应用
分析:利用绝对值三角不等式可得(|x+1|-|x-2|)max=3,依题意知,a≥(|x+1|-|x-2|)max,从而可得答案.
解答:
解:因为|x+1|-|x-2|≤|(x+1)+(2-x)|=3,即(|x+1|-|x-2|)max=3,
又不等式|x+1|-|x-2|≤a对于任意实数x恒成立,
所以a≥(|x+1|-|x-2|)max=3,
故答案为:a≥3.
又不等式|x+1|-|x-2|≤a对于任意实数x恒成立,
所以a≥(|x+1|-|x-2|)max=3,
故答案为:a≥3.
点评:本题考查绝对值不等式的解法,突出考查绝对值三角不等式的应用,求得(|x+1|-|x-2|)max=3是关键,属于中档题.

练习册系列答案
相关题目
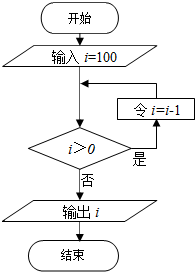
在如图程序框图的结构中最突出的逻辑结构及输出的i的值是( )

| A、当型循环结构,-1 |
| B、直到型循环结构,-1 |
| C、当型循环结构,0 |
| D、直到型循环结构,0 |
已知定点M(x0,y0)在直线l:f(x,y)=0外,则方程f(x,y)=f(x0,y0)表示( )
| A、与l重合的直线 |
| B、与l平行的直线 |
| C、与l垂直的直线 |
| D、点M(x0,y0) |
△ABC中,已知b=15,c=30,C=123°,则此三角形的解的情况是( )
| A、一解 | B、二解 |
| C、无解 | D、无法确定 |
已知函数f(x)是R上的增函数,A(0,-2),B(4,2)是其图象上的两点,那么|f(
)|<2的解集是( )
| 1 |
| 2x+1 |
| A、(1,4) |
| B、(1,+∞) |
| C、(-∞,1)∪[4,+∞] |
| D、(-3,+∞) |