题目内容

已知x、y满足不等式组
x+2y-3≤0
x+3y-2≥0
y≤1
，则z=x-y的最大值是（　　）
A、6B、4C、OD、-2
考点：简单线性规划
专题：数形结合,不等式的解法及应用
分析：由约束条件作出可行域，数形结合得到最优解，联立方程组求得最优解的坐标，代入目标函数求得z=x-y的最大值．
解答： 解：由约束条件
x+2y-3≤0
x+3y-2≥0
y≤1
作出可行域如图，

联立
x+2y-3=0
x+3y-2=0
，解得
x=5
y=-1
，∴A（5，-1）．
由z=x-y，得y=x-z，
由图可知，当直线y=x-z过A时，直线在y轴上的截距最小，z有最大值为5-（-1）=6．
故选：A．
点评：本题考查了简单的线性规划，考查了数形结合的解题思想方法，是中档题．
练习册系列答案
相关题目
已知2lgx=lg81，则x=
 
．
已知函数y=f（x）是函数y=log2x的反函数，
（Ⅰ）求y=f（x）的解析式．
（Ⅱ）若x∈（0，+∞），试分别写出使不等式
（ⅰ）log2x＜2x＜x2
（ⅱ）log2x＜x2＜2x成立自变量x的取值范围
（Ⅲ）求不等式loga（x-3）＞loga（5-x）的解集．
设F1、F2是双曲线C：
x2
a2
-
y2
b2
=1（a＞0，b＞0）的两个焦点，P是C上一点，若|PF1|+|PF2|=6a，且△PF1F2最小内角的大小为30°，则双曲线C的渐近线方程是（　　）
A、
2
x±y=0
B、x±
2
y=0
C、x±2y=0
D、2x±y=0
函数f（x）=ax+3•ex的图象存在与直线2x-4y+1=0垂直的切线，则实数a的取值范围是
 
．
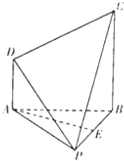已知直角梯形ABCD与等腰直角△APB所在平面互相垂直，AD∥BC，∠APB=∠ABC=90°，AB=BC=2AD=2，E为PB的中点．
（Ⅰ）求证：直线AE∥平面PCD；
（Ⅱ）求四面体C-PBD的体积．
如图所示的程序框图中，若f（x）=x2-x+1，g（x）=x+4，且h（x）≥m恒成立，则m的最大值是（　　）
A、4B、3C、1D、0
在△ABC中，P是BC的中点，AB=1，AC=2，则
AP
•
BC
=
 
．
在下列函数中．在[0，3]上是增函数且是偶函数的函数是（　　）
A、y=3x+3-x
B、y=-|x-3|
C、y=log2
3-x
3+x
D、y=cosx

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网