题目内容
在下列函数中.在[0,3]上是增函数且是偶函数的函数是( )
| A、y=3x+3-x | ||
| B、y=-|x-3| | ||
C、y=log2
| ||
| D、y=cosx |
考点:函数单调性的判断与证明,函数奇偶性的判断
专题:函数的性质及应用,导数的综合应用
分析:根据函数导数符号和函数单调性的关系,偶函数的定义,余弦函数的单调性即可判断每个选项的正误.
解答:
解:A.y′=ln3(3x-3-x);
∵x∈[0,3];
∴3x≥1,3-x≤1;
∴y′≥0;
∴该函数在[0,3]上是增函数,并且该函数是偶函数;
所以该选项正确;
B.设y=f(x),f(-1)=-4,f(1)=-2;
显然该函数不是偶函数;
∴该选项错误;
C.设y=f(x),则:
f(-x)=log2
=-log2
=-f(x);
∴该函数不是偶函数,所以该选项错误;
D.y=cosx在[0,π]上是减函数;
∴该函数在[0,3]上是减函数,所以该选项错误.
故选A.
∵x∈[0,3];
∴3x≥1,3-x≤1;
∴y′≥0;
∴该函数在[0,3]上是增函数,并且该函数是偶函数;
所以该选项正确;
B.设y=f(x),f(-1)=-4,f(1)=-2;
显然该函数不是偶函数;
∴该选项错误;
C.设y=f(x),则:
f(-x)=log2
| 3+x |
| 3-x |
| 3-x |
| 3+x |
∴该函数不是偶函数,所以该选项错误;
D.y=cosx在[0,π]上是减函数;
∴该函数在[0,3]上是减函数,所以该选项错误.
故选A.
点评:考查函数导数符号和函数单调性的关系,偶函数的定义,以及余弦函数的单调性.

练习册系列答案
相关题目
已知x、y满足不等式组
,则z=x-y的最大值是( )
|
| A、6 | B、4 | C、O | D、-2 |
一个几何体的三视图如图所示,且其侧(左)视图是一个等边三角形,则这个几何体的体积为( )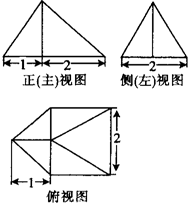

A、
| ||||
B、
| ||||
C、2
| ||||
D、
|
等差数列{an}的前n项和为Sn.若S19为一确定常数,下列各式也为确定常数的是( )
| A、a2+an |
| B、a2a17 |
| C、a1+a10+a19 |
| D、a1a10a19 |