题目内容
函数f(x)=ax+3•ex的图象存在与直线2x-4y+1=0垂直的切线,则实数a的取值范围是 .
考点:利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:求出原函数的导函数,由其导数等于-2得到a=3•ex-2有解,转化为求函数y=3•ex-2的值域得答案.
解答:
解:由f(x)=ax+3•ex,得f′(x)=a+3•ex,
∵函数f(x)=ax+3•ex的图象存在与直线2x-4y+1=0垂直的切线,
且直线2x-4y+1=0的斜率为
,
∴方程a+3•ex=-2有实数解,
即a=3•ex-2有解.
∵3•ex<0,∴a=3•ex-2<-2.
故答案为(-∞,-2).
∵函数f(x)=ax+3•ex的图象存在与直线2x-4y+1=0垂直的切线,
且直线2x-4y+1=0的斜率为
| 1 |
| 2 |
∴方程a+3•ex=-2有实数解,
即a=3•ex-2有解.
∵3•ex<0,∴a=3•ex-2<-2.
故答案为(-∞,-2).
点评:本题考查了利用导数研究过曲线上某点处的切线方程,考查了方程有解的条件,体现了数学转化思想方法,是中档题.

练习册系列答案
相关题目
设
为复数z=
-i的共轭复数,(z-
)2014=( )
. |
| z |
| 1 |
| 2 |
. |
| z |
| A、22014 |
| B、-22014 |
| C、22014i |
| D、-i |
设函数f(x)=n-1,x∈[n,n+1),n∈N,函数g(x)=log2x,则方程f(x)=g(x)实数根的个数是( )
| A、1个 | B、2个 | C、3个 | D、4个 |
O是平面上一点,A、B、C是平面上不共线三点,动点P满足:
=
+λ(
+
),λ∈[-1,2],已知λ=1时,|
|=2,则
•
+
•
的最大值为( )
| OP |
| OA |
| AB |
| AC |
| AP |
| PA |
| PB |
| PA |
| PC |
| A、-2 | B、24 | C、48 | D、96 |
已知x、y满足不等式组
,则z=x-y的最大值是( )
|
| A、6 | B、4 | C、O | D、-2 |
若函数f(x)=sinωx+
cosωx,x∈R,又f(a)=2,f(β)=0,|α-β|的最小值等于
,则正数ω的值为( )
| 3 |
| 5π |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
一个几何体的三视图如图所示,且其侧(左)视图是一个等边三角形,则这个几何体的体积为( )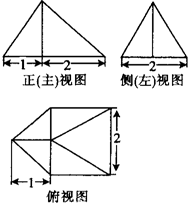

A、
| ||||
B、
| ||||
C、2
| ||||
D、
|
