题目内容
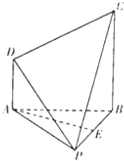 已知直角梯形ABCD与等腰直角△APB所在平面互相垂直,AD∥BC,∠APB=∠ABC=90°,AB=BC=2AD=2,E为PB的中点.
已知直角梯形ABCD与等腰直角△APB所在平面互相垂直,AD∥BC,∠APB=∠ABC=90°,AB=BC=2AD=2,E为PB的中点.(Ⅰ)求证:直线AE∥平面PCD;
(Ⅱ)求四面体C-PBD的体积.
考点:棱柱、棱锥、棱台的体积,直线与平面平行的判定
专题:空间位置关系与距离
分析:(Ⅰ)取PC的中点F,连结EF,DF,由已知得四边形AEFD为平行四边形,由此能证明AE∥平面PCD.
(2)取AB中点O,连结PO,由已知得PO⊥面ABCD,由VC-PBD=VP-BCD,利用等积法能求出四面体C-PBD的体积.
(2)取AB中点O,连结PO,由已知得PO⊥面ABCD,由VC-PBD=VP-BCD,利用等积法能求出四面体C-PBD的体积.
解答:
 (Ⅰ)证明:如图,取PC的中点F,连结EF,DF,
(Ⅰ)证明:如图,取PC的中点F,连结EF,DF,
在△PBC中,PE=EB,PF=FC,
∴EF
BC,又EF
BC,∴EF
AD,
∴四边形AEFD为平行四边形,
∴AE∥DF,又AE?平面PCD,DF?平面PCD,
∴AE∥平面PCD.
(2)如图,取AB中点O,连结PO,
在△APB中,AP=PB,∠APB=90°,
∴PO⊥AB,且PO=
AB=1,
又∵面APB⊥面ABCD,面APB∩面ABCD=AB,
∴PO⊥面ABCD,
在直角梯形ABCD中,S△BCD=
×BC×AB=
×2×2=2,
∴四面体C-PBD的体积VC-PBD=VP-BCD=
S△BCD×PO=
×2×1=
.
 (Ⅰ)证明:如图,取PC的中点F,连结EF,DF,
(Ⅰ)证明:如图,取PC的中点F,连结EF,DF,
在△PBC中,PE=EB,PF=FC,
∴EF
| ∥ |
. |
| 1 |
| 2 |
| ∥ |
. |
| 1 |
| 2 |
| ∥ |
. |
∴四边形AEFD为平行四边形,
∴AE∥DF,又AE?平面PCD,DF?平面PCD,
∴AE∥平面PCD.
(2)如图,取AB中点O,连结PO,
在△APB中,AP=PB,∠APB=90°,
∴PO⊥AB,且PO=
| 1 |
| 2 |
又∵面APB⊥面ABCD,面APB∩面ABCD=AB,
∴PO⊥面ABCD,
在直角梯形ABCD中,S△BCD=
| 1 |
| 2 |
| 1 |
| 2 |
∴四面体C-PBD的体积VC-PBD=VP-BCD=
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
点评:本题考查直线与平面平行的证明,考查四面体的体积的求法,解题时要注意空间思维能力的培养.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
已知x、y满足不等式组
,则z=x-y的最大值是( )
|
| A、6 | B、4 | C、O | D、-2 |
已知
,
,
均为非零向量,给出下列说法
①0•
=0②(
•
)•
=
•(
•
)③若
∥
,
∥
,则
∥
④若
⊥
,则|
+
|=|
-
|;⑤若(
+
)•(
-
)=0,则
=±
其中正确的个数是( )
| a |
| b |
| c |
①0•
| a |
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| b |
| c |
| a |
| c |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
其中正确的个数是( )
| A、1 | B、2 | C、3 | D、4 |
函数f(x)=2x+x的零点所在的区间是( )
A、(-1,-
| ||
B、(-
| ||
C、(0,
| ||
D、(
|
等差数列{an}的前n项和为Sn.若S19为一确定常数,下列各式也为确定常数的是( )
| A、a2+an |
| B、a2a17 |
| C、a1+a10+a19 |
| D、a1a10a19 |
 如图,已知F是菱形ABCD的对角线的交点,平面ABCD⊥平面DEC,ED=
如图,已知F是菱形ABCD的对角线的交点,平面ABCD⊥平面DEC,ED=