题目内容
已知函数y=f(x)是函数y=log2x的反函数,
(Ⅰ)求y=f(x)的解析式.
(Ⅱ)若x∈(0,+∞),试分别写出使不等式
(ⅰ)log2x<2x<x2
(ⅱ)log2x<x2<2x成立自变量x的取值范围
(Ⅲ)求不等式loga(x-3)>loga(5-x)的解集.
(Ⅰ)求y=f(x)的解析式.
(Ⅱ)若x∈(0,+∞),试分别写出使不等式
(ⅰ)log2x<2x<x2
(ⅱ)log2x<x2<2x成立自变量x的取值范围
(Ⅲ)求不等式loga(x-3)>loga(5-x)的解集.
考点:反函数
专题:函数的性质及应用
分析:(Ⅰ)根据指数对数函数的关系判断,
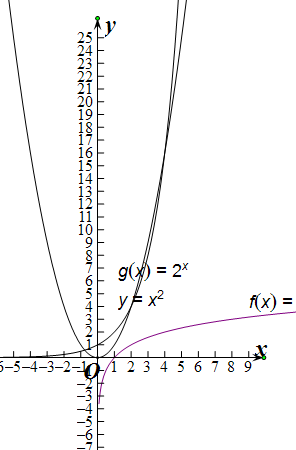
(Ⅱ)画出图象y=2x,y=x2,y=log2x,判断log2x<2x<x2,log2x<x2<2x,解集.
(Ⅲ)分类当a>1时,
当0<a<1时,
,
解得即可.
(Ⅱ)画出图象y=2x,y=x2,y=log2x,判断log2x<2x<x2,log2x<x2<2x,解集.
(Ⅲ)分类当a>1时,
|
|
解得即可.
解答:
 解:(Ⅰ)∵函数y=f(x)是函数y=log2x的反函数,
解:(Ⅰ)∵函数y=f(x)是函数y=log2x的反函数,
∴f(x)=2x,
(Ⅱ)y=2x,y=x2,y=log2x,
可得:22=4,24=42=16,
(i)∵log2x<2x<x2
∴2<x<4,
解集为:(2,4)
(ii)∵log2x<x2<2x,
∴0<x<2,或x>4,
解集为:(0,2)∪(4,+∞)
(Ⅲ)∵loga(x-3)>loga(5-x)
∴当a>1时,
解得;4<x<5,
∴当a>1时,解集为(4,5)
∵当0<a<1时,
,解得;3<x<4,
∴当0<a<1时,解集为(3,4)
 解:(Ⅰ)∵函数y=f(x)是函数y=log2x的反函数,
解:(Ⅰ)∵函数y=f(x)是函数y=log2x的反函数,∴f(x)=2x,
(Ⅱ)y=2x,y=x2,y=log2x,
可得:22=4,24=42=16,
(i)∵log2x<2x<x2
∴2<x<4,
解集为:(2,4)
(ii)∵log2x<x2<2x,
∴0<x<2,或x>4,
解集为:(0,2)∪(4,+∞)
(Ⅲ)∵loga(x-3)>loga(5-x)
∴当a>1时,
|
∴当a>1时,解集为(4,5)
∵当0<a<1时,
|
∴当0<a<1时,解集为(3,4)
点评:本题考查了函数的性质图象,不等式的求解,分类讨论,属于中档题.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
在(
+
)12的展开式中,x项的系数为( )
| x |
| 1 | |||
|
A、C
| ||
B、C
| ||
C、C
| ||
D、C
|
设函数f(x)=n-1,x∈[n,n+1),n∈N,函数g(x)=log2x,则方程f(x)=g(x)实数根的个数是( )
| A、1个 | B、2个 | C、3个 | D、4个 |
已知x、y满足不等式组
,则z=x-y的最大值是( )
|
| A、6 | B、4 | C、O | D、-2 |
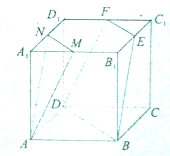 棱长为a的正方体ABCD-A1B1C1D1中,M、N、E、F分别为棱A1B1、A1D1、C1D1、B1C1的中点.
棱长为a的正方体ABCD-A1B1C1D1中,M、N、E、F分别为棱A1B1、A1D1、C1D1、B1C1的中点.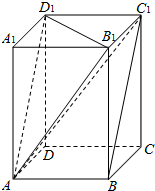 如图,正四棱柱ABCD-A1B1C1D1的底面边长为1,异面直线AD与BC1所成角的大小为60°,求:
如图,正四棱柱ABCD-A1B1C1D1的底面边长为1,异面直线AD与BC1所成角的大小为60°,求: 如图,已知F是菱形ABCD的对角线的交点,平面ABCD⊥平面DEC,ED=
如图,已知F是菱形ABCD的对角线的交点,平面ABCD⊥平面DEC,ED=