题目内容
5.设集合B={x|x<-1或x>16}.(1)求∁RB;
(2)设集合C={x|-2≤x<3},求(∁RB)∪C;
(3)设集合A={x|2a+1≤x≤3a-5},若A∩B=∅,求a的取值范围.
分析 (1)根据补集的定义进行求解;
(2)根据补集、并集的定义进行计算;
(3)根据A∩B=∅,对A进行讨论即可.
解答 解:(1)∵B={x|x<-1或x>16}.
∴∁RB={x|-1≤x≤16};
(2)∵∁RB={x|-1≤x≤16},
∴(∁RB)∪C={x|-2≤x≤16};
(3)若A∩B=∅,
∴若B=∅,即2a+1>3a-5得a<6;
若B≠∅,即a≥6时,则满足$\left\{\begin{array}{l}{3a-5≤16}\\{2a+1≥-1}\end{array}\right.$,
即$\left\{\begin{array}{l}{a≤7}\\{a≥-1}\end{array}\right.$,得-1≤a≤7,
此时6≤a≤7,
综上a≤7,即实数a的取值范围是{a|a≤7}.
点评 本题主要考查集合的基本运算,根据补集,并集以及交集的定义和性质是解决本题的关键.

练习册系列答案
相关题目
13.已知抛物线C:y2=4x的焦点为F,点P(2,t)为抛物线C上一点,则|PF|等于( )
| A. | 2 | B. | 3 | C. | 4 | D. | 6 |
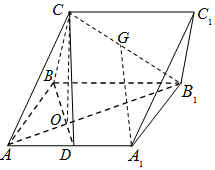 在三棱柱ABC-A1B1C1中,侧面ABB1A1为矩形,AB=2,AA1=2$\sqrt{2}$,D是AA1的中点,BD与AB1交于点O,且OC⊥平面ABB1A1.
在三棱柱ABC-A1B1C1中,侧面ABB1A1为矩形,AB=2,AA1=2$\sqrt{2}$,D是AA1的中点,BD与AB1交于点O,且OC⊥平面ABB1A1.