题目内容
18.已知点P(2,-1).(1)若一条直线经过点P,且原点到直线的距离为2,求该直线的一般式方程;
(2)求过点P且与原点距离最大的直线的一般式方程,并求出最大距离是多少?
分析 (1)当l的斜率k不存在时,直接写出直线方程;当l的斜率k存在时,设l:y+1=k(x-2),即kx-y-2k-1=0.由点到直线的距离公式求得k值,则直线方程可求;
(2)由题意可得过P点与原点O距离最大的直线是过P点且与PO垂直的直线,求出OP所在直线的斜率,进一步得到直线l的斜率,得到直线l的方程,再由点到直线的距离公式得最大距离.
解答 解:(1)①当l的斜率k不存在时,l的方程为x=2;
②当l的斜率k存在时,设l:y+1=k(x-2),即kx-y-2k-1=0.
由点到直线距离公式得$\frac{{|{-2k-1}|}}{{\sqrt{1+{k^2}}}}=2$,得l:3x-4y-10=0.
故所求l的方程为:x=2 或 3x-4y-10=0;
(2)由题意可得过P点与原点O距离最大的直线是过P点且与PO垂直的直线,
由l⊥OP,得klkOP=-1,kl=$-\frac{1}{{{k_{op}}}}=2$,
由直线方程的点斜式得y+1=2(x-2),即2x-y-5=0.
即直线2x-y-5=0是过P点且与原点O距离最大的直线,最大距离为 $\frac{{|{-5}|}}{{\sqrt{5}}}=\sqrt{5}$.
点评 本题考查直线的点斜式方程,考查点到直线的距离公式的应用,属中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.已知函数f(x)是定义在R上的偶函数,且在(-∞,0]上单调递减,若f(-1)=0,则不等式f(2x-1)>0解集为( B )( )
| A. | (-6,0)∪(1,3) | B. | (-∞,0)∪(1,+∞) | C. | (-∞,1)∪(3,+∞) | D. | (-∞,-1)∪(3,+∞) |
7.函数$f(x)=\left\{\begin{array}{l}0,(x>0)\\ π,(x=0)\\ 1,(x<0)\end{array}\right.$,则f(f(f(π)))=( )
| A. | 1 | B. | 0 | C. | π | D. | π+1 |
8.已知集合P={y|y=($\frac{1}{2}$)x,x>0},Q={x|y=lg(2x-x2)},则∁RP∩Q=( )
| A. | [1,2) | B. | (1,+∞) | C. | [2,+∞) | D. | [1,+∞) |
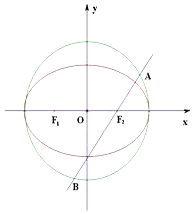 已知椭圆的标准方程为:$\frac{{x}^{2}}{4{a}^{2}}$+$\frac{{y}^{2}}{3{a}^{2}}$=1(a>0)
已知椭圆的标准方程为:$\frac{{x}^{2}}{4{a}^{2}}$+$\frac{{y}^{2}}{3{a}^{2}}$=1(a>0)