题目内容
7.函数$f(x)=\left\{\begin{array}{l}0,(x>0)\\ π,(x=0)\\ 1,(x<0)\end{array}\right.$,则f(f(f(π)))=( )| A. | 1 | B. | 0 | C. | π | D. | π+1 |
分析 先求出f(π)=0,从而f(f(π))=f(0)=π,进而f(f(f(π)))=f(π),由此能求出结果.
解答 解:∵函数$f(x)=\left\{\begin{array}{l}0,(x>0)\\ π,(x=0)\\ 1,(x<0)\end{array}\right.$,
∴f(π)=0,
f(f(π))=f(0)=π
f(f(f(π)))=f(π)=0.
故选:B.
点评 本题考查函数值的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
17.已知集合$A=\{y|y=\sqrt{x}\}$,B={x|y=ln(1-x)},则A∩B=( )
| A. | {x|0≤x<e} | B. | {x|0≤x<1} | C. | {x|1≤x<e} | D. | {x|x≥0} |
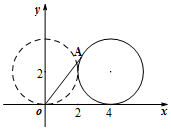 如图,半径为2的圆圆心的初始位置坐标为(0,2),圆上一点A坐标为(0,0).圆沿x轴正向滚动,当圆滚动到圆心位于(4,2)时,A点坐标为(4-2sin2,2-2cos2).
如图,半径为2的圆圆心的初始位置坐标为(0,2),圆上一点A坐标为(0,0).圆沿x轴正向滚动,当圆滚动到圆心位于(4,2)时,A点坐标为(4-2sin2,2-2cos2).