Question

8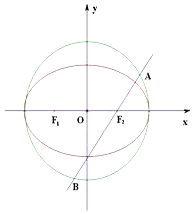．已知椭圆的标准方程为：$\frac{{x}^{2}}{4{a}^{2}}$+$\frac{{y}^{2}}{3{a}^{2}}$=1（a＞0）
（1）当a=1时，求椭圆的焦点坐标及椭圆的离心率；
（2）过椭圆的右焦点F₂的直线与圆C：x²+y²=4a²（常数a＞0）交于A，B两点，求|F₂A|•|F₂B|的值．

Answer 1

分析 （1）当a=1时，$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$，a=2，b=$\sqrt{3}$，c=1，焦点坐标F₁（-1，0），F₂（1，0），离心率e=$\frac{c}{a}$=$\frac{1}{2}$；
（2）当斜率不存在时，丨F₁A丨=丨F₁B丨=$\sqrt{3}$a，此时|F₂A|•|F₂B|=3a²；当斜率不存在时，AB：y=k（x-a），代入圆方程，由韦达定理及两点之间的距离公式即可|F₂A|•|F₂B|的值．

解答 解：（1）当a=1时，$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$，a=2，b=$\sqrt{3}$，c=1，焦点坐标F₁（-1，0），F₂（1，0），…（2分）
离心率e=$\frac{c}{a}$=$\frac{1}{2}$；…（3分）
（2）当斜率不存在时，丨F₁A丨=丨F₁B丨=$\sqrt{4{a}^{2}-{a}^{2}}$=$\sqrt{3}$a
此时|F₂A|•|F₂B|=3a²；                 （5分）
当斜率不存在时，AB：y=k（x-a），设A（x₁，y₁），B（x₂，y₂），
由$\left\{\begin{array}{l}{y=k（x-a）}\\{{x}^{2}+{y}^{2}=4{a}^{2}}\end{array}\right.$，整理得：（1+k²）x²-2ak²x+k²a²-4a²=0，（7分）
x₁+x₂=$\frac{2a{k}^{2}}{1+{k}^{2}}$，x₁x₂=$\frac{{k}^{2}{a}^{2}-4{a}^{2}}{1+{k}^{2}}$，（9分）
丨F₁A丨=$\sqrt{（{x}_{1}-a）^{2}+{y}_{1}^{2}}$=$\sqrt{1+{k}^{2}}$•丨x₁-a丨，丨F₂A丨=$\sqrt{1+{k}^{2}}$•丨x₂-a丨，
∴|F₂A|•|F₂B|=（1+k²）丨x₁x₂-a（x₁+x₂）+a²丨，
=（1+k²）丨$\frac{{k}^{2}{a}^{2}-4{a}^{2}}{1+{k}^{2}}$-$\frac{2{a}^{2}{k}^{2}}{1+{k}^{2}}$+a²丨，
=3a²，（11分）                
∴|F₂A|•|F₂B|为定值3a²．（12分）

点评 本题考查椭圆的标准方程及性质，直线与圆的位置关系，韦达定理，两点间的距离公式，考查计算能力，属于中档题．