题目内容
3.已知等边三角形的边长为a,P是△ABC所在平面上的一点,求|PA|2+|PB|2+|PC|2的最小值.分析 本题可以先建立坐标系,利用两点距离公式将PA2+PB2+PC2转化为两二次函数式的和,再分别求它们的最值,得到本题结论.
解答 解:建立平面直角坐标系,设A(x1,y1),B(x2,y2),C(x3,y3),P(x,y),
则有:PA2+PB2+PC2=(x-x1)2+(y-y1)2+(x-x2)2+(y-y2)2+(x-x3)2+(y-y3)2
=3x2-2(x1+x2+x3)x+${{x}_{1}}^{2}$+${{x}_{2}}^{2}$+${{x}_{3}}^{2}$+3y2-2(y1+y2+y3)y+${{y}_{1}}^{2}$+${{y}_{2}}^{2}$+${{y}_{3}}^{2}$,
记f(x)=3x2-2(x1+x2+x3)x+${{x}_{1}}^{2}$+${{x}_{2}}^{2}$+${{x}_{3}}^{2}$,
当且仅当x=$\frac{{x}_{1}{+x}_{2}{+x}_{3}}{3}$时,f(x)取最小值;
记g(y)=3y2-2(y1+y2+y3)y+${{y}_{1}}^{2}$+${{y}_{2}}^{2}$+${{y}_{3}}^{2}$,
当且仅当y=$\frac{{y}_{1}+{{y}_{2}+y}_{3}}{3}$时,g(y)取最小值.
∴当且仅当x=$\frac{{x}_{1}{+x}_{2}{+x}_{3}}{3}$,y=$\frac{{y}_{1}+{{y}_{2}+y}_{3}}{3}$时,PA2+PB2+PC2取最小值,
此时,P为正△ABC的重心.
∵正△ABC的边长为a,
∴PA2+PB2+PC2=($\frac{\sqrt{3}}{3}$a)2+($\frac{\sqrt{3}}{3}$a)2+($\frac{\sqrt{3}}{3}$a)2=a2,
∴PA2+PB2+PC2≥a2,此时,P为正△ABC的重心,
∴|PA|2+|PB|2+|PC|2的最小值是a2.
点评 本题考查了两点间距离公式,还考查了解析法研究问题的思想和方法,有一定的思维难度,属于中档题.

| A. | f(1) | B. | f(2) | C. | f(3) | D. | f(4) |
| A. | 0.76<log0.76<60.7 | B. | log0.76<0.76<60.7 | ||
| C. | log0.76<60.7<0.76 | D. | 0.76<60.7<log0.76 |
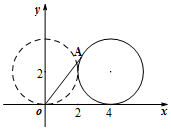 如图,半径为2的圆圆心的初始位置坐标为(0,2),圆上一点A坐标为(0,0).圆沿x轴正向滚动,当圆滚动到圆心位于(4,2)时,A点坐标为(4-2sin2,2-2cos2).
如图,半径为2的圆圆心的初始位置坐标为(0,2),圆上一点A坐标为(0,0).圆沿x轴正向滚动,当圆滚动到圆心位于(4,2)时,A点坐标为(4-2sin2,2-2cos2).