题目内容
定义运算“*”如下：a*b=
，则函数f（x）=（1*x）•x-（2*x）（x∈[-2，2]）的最大值为（ ）
|
| A、12 | B、10 | C、8 | D、6 |
考点：分段函数的应用
专题：函数的性质及应用
分析：根据定义求出函数f（x）的表达式，即可得到结论．
解答：
解：∵x∈[-2，2]，∴2*x=2，即f（x）=（1*x）•x-（2*x）=（1*x）•x-2，
当-2≤x≤1时，f（x）=（1*x）•x-2=x-2，此时-4≤f（x）≤-1，
当1＜x≤2时，f（x）=（1*x）•x-2=x3-2，此时-1＜f（x）≤6，
故函数f（x）的最大值为6，
故选：D
当-2≤x≤1时，f（x）=（1*x）•x-2=x-2，此时-4≤f（x）≤-1，
当1＜x≤2时，f（x）=（1*x）•x-2=x3-2，此时-1＜f（x）≤6，
故函数f（x）的最大值为6，
故选：D
点评：本题主要考查函数最值的求解，根据定义求出函数f（x）的表达式结合二次函数的图象和性质是解决本题的关键．
练习册系列答案
小学学习好帮手系列答案
小学同步三练核心密卷系列答案
相关题目
下列命题中，
①若
与
互为相反向量，则
+
=0；
②若k为实数，且k•
=
，则
=
或k=0；
③若
•
=0，则
=0或
=0；
④若
与
为平行的向量，则
•
=|
|•|
|；
⑤若|
|=1，则
=±1．
其中假命题的个数为（ ）
①若
| a |
| b |
| a |
| b |
②若k为实数，且k•
| a |
| 0 |
| a |
| 0 |
③若
| a |
| b |
| a |
| b |
④若
| a |
| b |
| a |
| b |
| a |
| b |
⑤若|
| a |
| a |
其中假命题的个数为（ ）
| A、5个 | B、4个 | C、3个 | D、2个 |
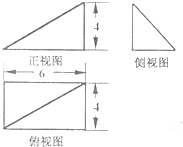
如图，四边形BCDE是直角梯形，CD∥BE，CD丄BC，CD=