题目内容
 如图,四边形BCDE是直角梯形,CD∥BE,CD丄BC,CD=
如图,四边形BCDE是直角梯形,CD∥BE,CD丄BC,CD=| 1 |
| 2 |
(1)求直线CD与平面DFM所成角的正弦值;
(2)能否在线段EM上找到一点G,使得FG丄平面BCDE?若能,请指出G的位置,
并加以证明;若不能,请说明理由;
(3)求三棱锥F-DME的体积.
考点:棱柱、棱锥、棱台的体积,直线与平面所成的角
专题:综合题,空间位置关系与距离,空间角
分析:(1)证明EB⊥平面ABC,以B为坐标原点建立如图所示的空间直角坐标系B-xyz,求出平面DFM的法向量,利用向量的夹角公式,即可求直线CD与平面DFM所成角的正弦值;
(2)设存在点G满足题设,且
=λ
=(0≤λ≤1).利用
•
=16λ-8=0,得λ=
.即可得出结论;
(3)求出S△DME=6
,由(2)知,FG为三棱锥的高,FG=
,即可求三棱锥F-DME的体积.
(2)设存在点G满足题设,且
| EG |
| EM |
| FG |
| EM |
| 1 |
| 2 |
(3)求出S△DME=6
| 2 |
| 2 |
解答:
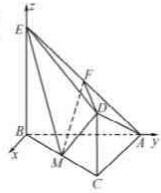 解:由题意,CD⊥BC.四边形BCDE是直角梯形,EB⊥BC.
解:由题意,CD⊥BC.四边形BCDE是直角梯形,EB⊥BC.
又平面BCDE⊥平面ABC,∴EB⊥平面ABC.
于是以B为坐标原点建立如图所示的空间直角坐标系B-xyz.
则B(0,0,0),C(4,4,0),A(0,4,0),D(4,4,2),E(0,0,4),F(0,2,2),M(2,2,0
(1)
=(0,0,2).
设
=(x,y,z)为平面DFM的法向量.
得
,令x=1,得
=(1,-2,1).
于是sinθ=
;
(2)证明:设存在点G满足题设,且
=λ
=(0≤λ≤1).
则G(2λ,2λ,4-4λ),
=(2λ,2λ-2,2-4λ).
由
•
=16λ-8=0,得λ=
.经检验
•
=0.
故当G为EM的中点时,FG⊥平面BCDE.
(3)∵BE∥CD,CD⊥BC,且四边形BCDE是直角梯形,
∴S△BME=
×4×2
=4
,S△DCM=2
,
∵梯形BCDE的面积为
×(4+2)×4
=12
,
∴S△DME=6
,
由(2)知,FG为三棱锥的高,FG=
,
∴三棱锥F-DME的体积为
×6
×
=4.
 解:由题意,CD⊥BC.四边形BCDE是直角梯形,EB⊥BC.
解:由题意,CD⊥BC.四边形BCDE是直角梯形,EB⊥BC.又平面BCDE⊥平面ABC,∴EB⊥平面ABC.
于是以B为坐标原点建立如图所示的空间直角坐标系B-xyz.
则B(0,0,0),C(4,4,0),A(0,4,0),D(4,4,2),E(0,0,4),F(0,2,2),M(2,2,0
(1)
| CD |
设
| m |
得
|
| m |
于是sinθ=
| ||
| 6 |
(2)证明:设存在点G满足题设,且
| EG |
| EM |
则G(2λ,2λ,4-4λ),
| FG |
由
| FG |
| EM |
| 1 |
| 2 |
| FG |
| ED |
故当G为EM的中点时,FG⊥平面BCDE.
(3)∵BE∥CD,CD⊥BC,且四边形BCDE是直角梯形,
∴S△BME=
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
∵梯形BCDE的面积为
| 1 |
| 2 |
| 2 |
| 2 |
∴S△DME=6
| 2 |
由(2)知,FG为三棱锥的高,FG=
| 2 |
∴三棱锥F-DME的体积为
| 1 |
| 3 |
| 2 |
| 2 |
点评:本题考查求三棱锥F-DME的体积,考查空间角,正确运用空间向量是关键.

练习册系列答案
相关题目
一元二次方程2x2-6x-3=0的两根为x1,x2,则(1+x1)(1+x2)的值为( )
| A、3 | ||
| B、6 | ||
| C、-3 | ||
D、
|
下列选项中,可作为函数y=f(x)的图象的是( )
A、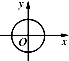 |
B、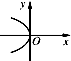 |
C、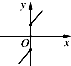 |
D、 |