题目内容
计算:log2
+lg20-lg2+3 log42-(-2)0.
| 8 |
考点:对数的运算性质
专题:计算题
分析:根据对数的运算性质,结合对数指数的互化,从而进行计算.
解答:
解:原式=
+1+lg2-lg2+
-1
=
+
.
| 3 |
| 2 |
| 3 |
=
| 3 |
| 2 |
| 3 |
点评:本题考查了对数的运算性质,考查了对数指数的相互转化,是一道基础题.

练习册系列答案
相关题目
已知集合A={x|y=
},B={y|y=3x,x<0},则A∩B=( )
| log3x+1 |
A、(
| ||
B、[
| ||
C、(0,
| ||
D、[
|
已知函数f(x)=
(x∈R),则下列结论中不正确的是( )
| x |
| 1+|x| |
| A、对任意x∈R,等式f(-x)+f(x)=0恒成立 |
| B、函数f(x)的值域为(-1,1) |
| C、对任意x1,x2∈R,若x1≠x2,则一定有f(x1)≠f(x2) |
| D、方程f(x)-x=0则R上有三个根 |
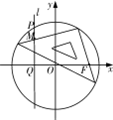 如图,设P是圆O:x2+y2=2上的点,过P作直线l垂直x轴于点Q,M为l上一点,且
如图,设P是圆O:x2+y2=2上的点,过P作直线l垂直x轴于点Q,M为l上一点,且