Question

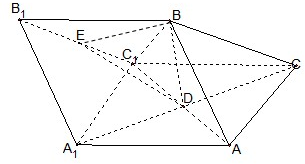如图，三棱柱ABC-A₁B₁C₁中，AB=AC=AA₁=BC₁=2，∠AA₁C₁=60°，平面ABC₁⊥平面AA₁C₁C，AC₁与A₁C相交于点D．
（1）求证：BD⊥平面AA₁C₁；
（2）（理）设点E是直线B₁C₁上一点，且DE∥平面AA₁B₁B，求平面EBD与平面ABC₁夹角的余弦值．

Answer 1

考点：与二面角有关的立体几何综合题,直线与平面垂直的判定

专题：空间角

分析：（1）由已知条件推导出BD⊥AC₁，由此能够证明BD⊥平面AA₁C₁C．
（2）以D为原点，以DA₁，DA，DB所在直线分别为x轴，y轴，z轴，建立空间直角坐标系，利用向量法能求出平面EBD与平面ABC₁夹角的余弦值．

解答： （1）证明：由已知得侧面AACC是菱形，D是AC₁的中点，
∵AB=AC=AA₁=BC₁=2，AC₁与A₁C相交于点D，
∴BD⊥AC₁，∵平面ABC₁⊥平面AA₁C₁C，且BD不包含于平面ABC₁，
平面ABC₁∩平面AA₁C₁C=AC₁，
∴BD⊥平面AA₁C₁C．
（2）（理）解：设点F是A₁C₁的中点，∵点D是AC₁的中点，∴DF∥平面AA₁B₁B，
又∵DE∥平面AA₁B₁B，∴平面DEF∥平面AA₁B₁B，
又平面DEF∩平面A₁B₁C₁=EF，平面AA₁B₁B∩平面A₁B₁C₁=A₁B₁，
∴EF∥A₁B₁，∴点E是B₁C₁的中点．
如图，以D为原点，以DA₁，DA，DB所在直线分别为x轴，y轴，z轴，
建立空间直角坐标系．
由已知得AC₁=2，AD=1，BD=A₁D=DC=

3

，BC=

6

∴D(0，0，0)，A(0，1，0)，A1(

3

，0，0)，B(0，0，

3

)，C1(0，-1，0)
设平面EBD的一个法向量是

m

=(x，y，z)，
由

m

⊥

DB

，得

3

z=0⇒z=0，
又

DE

=

1

2

(

DC1

+

DB1

)=

1

2

(

DC1

+

DB

+

AA1

)
=(

3

2

，-1，

3

2

)，
由

m

⊥

DE

⇒(x，y，z)•(

3

2

，-1，

3

2

)=0
得

3

2

x-y=0，
令x=1，得y=

3

2

，∴

m

=(1，

3

2

，0)，
∵平面ABC₁⊥平面AA₁C₁C，DA₁⊥AC₁，∴DA₁⊥平面ABC₁
∴平面ABC₁的一个法向量是

DA1

=(

3

，0，0)，
∵cos＜

m

，

DA1

＞=

3

1+ 3 4 × 3

=

2 7

7

，
∴平面EBD与平面ABC₁夹角的余弦值是

2 7

7

．

点评：本题考查直线与平面垂直的证明，考查二面角的余弦值的求法，解题时要认真审题，注意向量法的合理运用．