题目内容
椭圆上一点P与该椭圆的焦点F的连线与x轴垂直,如果椭圆的离心率e=
,P点到原点的距离为2
,椭圆的两轴都在坐标轴上,求椭圆的方程.
| ||
| 2 |
| 3 |
考点:椭圆的标准方程
专题:圆锥曲线的定义、性质与方程
分析:由已知条件设椭圆方程为
+
=1,由已知条件推导出
,由此能求出椭圆方程.
| x2 |
| a2 |
| y2 |
| b2 |
|
解答:
解:由已知条件设椭圆方程为
+
=1,
∵椭圆上一点P与该椭圆的焦点F的连线与x轴垂直,
椭圆的离心率e=
,P点到原点的距离为2
,
∴
,解得a=4,b=c=2
,
∴椭圆方程为
+
=1.
| x2 |
| a2 |
| y2 |
| b2 |
∵椭圆上一点P与该椭圆的焦点F的连线与x轴垂直,
椭圆的离心率e=
| ||
| 2 |
| 3 |
∴
|
| 2 |
∴椭圆方程为
| x2 |
| 16 |
| y2 |
| 8 |
点评:本题考查椭圆方程的求法,是中档题,解题时要认真审题,注意椭圆性质的灵活运用.

练习册系列答案
相关题目
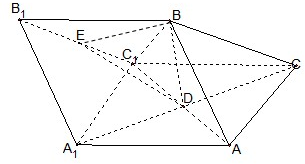 如图,三棱柱ABC-A1B1C1中,AB=AC=AA1=BC1=2,∠AA1C1=60°,平面ABC1⊥平面AA1C1C,AC1与A1C相交于点D.
如图,三棱柱ABC-A1B1C1中,AB=AC=AA1=BC1=2,∠AA1C1=60°,平面ABC1⊥平面AA1C1C,AC1与A1C相交于点D.