题目内容
已知集合M={x|x2-2x-3=0}，P={x|x+1≥0}，试判断M与P的关系．
考点：集合的包含关系判断及应用
专题：集合
分析：首先，化简集合M，P，然后，结合它们元素之间的关系进行判断即可．
解答：
解：由x2-2x-3=0得，M={-1，3}，
又集合P={x|x≥-1}，
∴M⊆P．
又集合P={x|x≥-1}，
∴M⊆P．
点评：本题重点考查集合之间的关系，属于基础题．
练习册系列答案
相关题目
设不等式x2-x≤0的解集为M，函数f（x）=lg（1-|x|）的定义域为N，则M∩N=（ ）
| A、（-1，0] |
| B、[0，1） |
| C、（0，1） |
| D、[0，1] |
如图所示的几何体中，四边形ABCD与DBFE均为菱形，∠DAB=∠DBF=60°，且FA=FC．
已知向量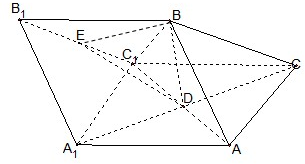
如图，三棱柱ABC-A1B1C1中，AB=AC=AA1=BC1=2，∠AA1C1=60°，平面ABC1⊥平面AA1C1C，AC1与A1C相交于点D．