题目内容
设变量x，y满足
，则2x+y的最大值和最小值分别为（ ）
|
| A、1，-1 | B、2，-2 |
| C、1，-2 | D、2，-1 |
考点：简单线性规划
专题：数形结合
分析：由不等式组作出可行域，令z=2x+y，数形结合求出z的最大值和最小值．
解答：
解：由
作可行域如图，
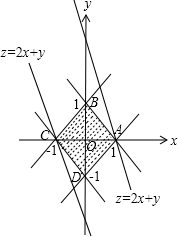
令z=2x+y，则y=-2x+z，
由图可知，当y=-2x+z过A（1，0）时，截距z最大，最大值为z=2×1+0=2；
当y=-2x+z过C（-1，0）时，截距z最小，最小值为z=-2×1+0=-2．
∴2x+y的最大值和最小值分别为2，-2．
故选：B．
|
令z=2x+y，则y=-2x+z，
由图可知，当y=-2x+z过A（1，0）时，截距z最大，最大值为z=2×1+0=2；
当y=-2x+z过C（-1，0）时，截距z最小，最小值为z=-2×1+0=-2．
∴2x+y的最大值和最小值分别为2，-2．
故选：B．
点评：本题是直接考查线性规划问题，近年来高考线性规划问题高考数学考试的热点，数形结合是数学思想的重要手段之一，是连接代数和几何的重要方法．随着要求数学知识从书本到实际生活的呼声不断升高，线性规划这一类新型数学应用问题要引起重视．是中档题．
练习册系列答案
相关题目
已知M={（x，y）|y=2x}，N={（x，y）|y=a}，若M∩N=∅，则实数a的取值范围为（ ）
| A、（-∞，1） |
| B、（-∞，1] |
| C、（-∞，0） |
| D、（-∞，0] |
设不等式x2-x≤0的解集为M，函数f（x）=lg（1-|x|）的定义域为N，则M∩N=（ ）
| A、（-1，0] |
| B、[0，1） |
| C、（0，1） |
| D、[0，1] |
若函数f（x）=1-2sin2（x+
）（x∈R），则f（x）是（ ）
| π |
| 4 |
| A、最小正周期为π的偶函数 | ||
| B、最小正周期为π的奇函数 | ||
C、最小正周期为
| ||
D、最小正周期为
|
等差数列{an}中，an＞0，a12+a72+2a1a7=4，则它的前7项的和等于（ ）
A、
| ||
| B、5 | ||
C、
| ||
| D、7 |
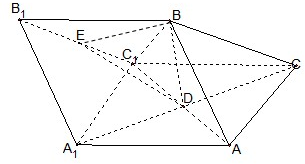如图，三棱柱ABC-A1B1C1中，AB=AC=AA1=BC1=2，∠AA1C1=60°，平面ABC1⊥平面AA1C1C，AC1与A1C相交于点D．