题目内容
随机向边长为2的正方形ABCD中投一点M,则点M与点A的距离不小于1且∠CMD为锐角的概率是 .
考点:几何概型
专题:概率与统计
分析:画出图形,结合图形,求出正方形ABCD的面积,满足条件的点M的面积是什么,求出对应的概率即可.
解答:
解:如图所示,
四边形ABCD是边长为2的正方形,其中的大圆弧是半径为1的圆面的
,
正方形的面积是4,
圆面的面积是
,
小圆弧所围成的图形是半径为1的圆面的一半,面积为
π,
∴阴影部分的面积是4-
-
π=4-
;
∴满足条件的点M的概率为
P=
=1-
.
故答案为:1-
.

四边形ABCD是边长为2的正方形,其中的大圆弧是半径为1的圆面的
| 1 |
| 4 |
正方形的面积是4,
| 1 |
| 4 |
| π |
| 4 |
小圆弧所围成的图形是半径为1的圆面的一半,面积为
| 1 |
| 2 |
∴阴影部分的面积是4-
| π |
| 4 |
| 1 |
| 2 |
| 3π |
| 4 |
∴满足条件的点M的概率为
P=
4-
| ||
| 4 |
| 3π |
| 16 |
故答案为:1-
| 3π |
| 16 |
点评:本题考查了几何概型的应用问题,解题时应画出图形,结合图形解答问题,是基础题.

练习册系列答案
相关题目
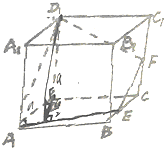 已知E、F分别为正方体ABCD-A1B1C1D1的棱BC,CC1的中点,设α为二面角D-AE-D1的平面角,求sinα=( )
已知E、F分别为正方体ABCD-A1B1C1D1的棱BC,CC1的中点,设α为二面角D-AE-D1的平面角,求sinα=( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知A、B、M三点不共线,对于平面ABM外任意一点O,若
+
=3
-
,则点P与A、B、M( )
| OB |
| OM |
| OP |
| OA |
| A、共面 | B、共线 |
| C、不共面 | D、不确定 |