题目内容
已知集合A={z|z=1+i+i2+…+in，n∈N*}，则集合A的子集个数为 ．
考点：子集与真子集
专题：集合
分析：先判断集合集合A中的元素的个数，再利用子集的个数公式进行进行求解；
解答：
解：∵集合A={z|z=1+i+i2+…+in，n∈N*}，取n=1，2，3，4…，
∴A={1+i，i，0，1}，一共有4个元素，
∴集合A的子集的个数为：24=16，
故答案为：16．
∴A={1+i，i，0，1}，一共有4个元素，
∴集合A的子集的个数为：24=16，
故答案为：16．
点评：本题考查集合的子集个数问题，对于集合M的子集问题一般来说，若M中有n个元素，则集合M的子集共有2n个．
练习册系列答案
阳光考场单元测试卷系列答案
名校联盟冲刺卷系列答案
名校提分一卷通系列答案
课程达标测试卷闯关100分系列答案
相关题目
已知函数f（x），x∈R，且在x=1处，f（x）存在极小值，则（ ）
| A、当x∈（-∞，1）时，f′（x）＞0；当x∈（1，+∞）时，f′（x）＜0 |
| B、当x∈（-∞，1）时，f′（x）＞0；当x∈（1，+∞）时，f′（x）＞0 |
| C、当x∈（-∞，1）时，f′（x）＜0；当x∈（1，+∞）时，f′（x）＞0 |
| D、当x∈（-∞，1）时，f′（x）＜0；当x∈（1，+∞）时，f′（x）＜0 |
函数f（x）=lg（x2-ax+3）的定义域为R，则实数a的取值范围是（ ）
A、[-2
| ||||
B、（-2
| ||||
C、（-∞，-2
| ||||
D、（-∞，-2
|
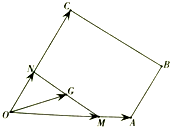如图，梯形OABC中，OA=OC=2AB=1，OC∥AB，∠AOC=