Question

19．如图，已知四棱锥A-CBB₁C₁的底面为矩形，D为AC₁的中点，AC⊥平面BCC₁B₁．
（Ⅰ）证明：AB∥平面CDB₁；
（Ⅱ）若AC=BC=1，BB₁=$\sqrt{3}$，
（1）求BD的长；
（2）求三棱锥C-DB₁C₁的体积．

Answer 1

分析 （Ⅰ）连结BC₁，B₁C连结DE，可得DE∥AB，即可得AB∥平面CDB₁；
（Ⅱ）（1）可得BC⊥CD，在RtBCD中，由BC=1，CD=$\frac{1}{2}A{C}_{1}$=$\frac{1}{2}\sqrt{A{C}^{2}+C{{C}_{1}}^{2}}$=1，可得BD
（2）V${\;}_{C-D{B}_{1}{C}_{1}}$=V${\;}_{{B}_{1}-CD{C}_{1}}$=$\frac{1}{2}{S}_{△CD{C}_{1}}•{B}_{1}{C}_{1}$=$\frac{1}{3}×\frac{1}{4}×1×\sqrt{3}×1=\frac{\sqrt{3}}{12}$

解答 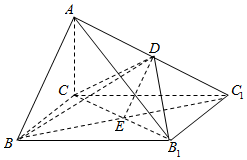解：（Ⅰ）证明：连结BC₁，B₁C连结DE，--------------------------（1分）
∵D、E分别为AC₁，BC₁，∴DE∥AB，-------------------------------（2分）
又∵DE?CDB₁ AB?CDB₁，∴AB∥平面CDB₁；---------------------------------（4分）
（Ⅱ）（1）∵AC⊥平面BCC₁B₁，BC?BCC₁B₁
∴BC⊥AC
∵BC⊥CC₁，AC∩CC₁=C
BC⊥平面ACC₁，CD?平面ACC₁
∴BC⊥CD------------------------------------------------------------------------------（6分）
在R△BCD中，∵BC=1，CD=$\frac{1}{2}A{C}_{1}$=$\frac{1}{2}\sqrt{A{C}^{2}+C{{C}_{1}}^{2}}$=1
∴$BD=\sqrt{2}$--------------------------------------------------（8分）
（2）∵BC⊥平面ACC₁，BC∥B₁C₁
∴B₁C₁⊥平面ACC₁，-----------------------------------------------------------------------------------------（10分）
∴V${\;}_{C-D{B}_{1}{C}_{1}}$=V${\;}_{{B}_{1}-CD{C}_{1}}$=$\frac{1}{2}{S}_{△CD{C}_{1}}•{B}_{1}{C}_{1}$=$\frac{1}{3}×\frac{1}{4}×1×\sqrt{3}×1=\frac{\sqrt{3}}{12}$-----------------------------（12分）

点评 本题考查了空间位置关系的判定，几何体体积的计算，属于中档题．