题目内容
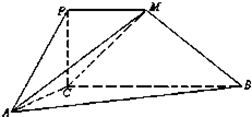 如图,四边形PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=1,BC=2.又AC=1,∠ACB=120°,AB⊥PC,直线AM与直线PC所成的角为60°.
如图,四边形PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=1,BC=2.又AC=1,∠ACB=120°,AB⊥PC,直线AM与直线PC所成的角为60°.(Ⅰ)求证:PC⊥AC;
(Ⅱ)求三棱锥VB-MAC的体积.
考点:棱柱、棱锥、棱台的体积
专题:综合题,空间位置关系与距离
分析:(Ⅰ)利用线面垂直的判定定理,证明PC⊥平面ABC,然后证明PC⊥AC;
(Ⅱ)由PC⊥平面ABC,根据面面垂直的判定可得面ABC⊥面PVBM,再由两面垂直的性质定理可得三棱锥A-MBC的高,解直角三角形求出三棱锥A-MBC的高,则体积可求.
(Ⅱ)由PC⊥平面ABC,根据面面垂直的判定可得面ABC⊥面PVBM,再由两面垂直的性质定理可得三棱锥A-MBC的高,解直角三角形求出三棱锥A-MBC的高,则体积可求.
解答:
(I)证明:∵PC⊥BC,PC⊥AB,BC∩AB=B,
∴PC⊥平面ABC,
∵AC?平面ABC,∴PC⊥AC.
(II)解:∵PC⊥平面ABC,PC?平面PCBM,∴平面PCBM⊥平面ABC,
如图, 在平面ABC中过A作AD垂直于BC的延长线与D,则AD⊥平面PCBM,则AD为三棱锥A-MBC的高,
在平面ABC中过A作AD垂直于BC的延长线与D,则AD⊥平面PCBM,则AD为三棱锥A-MBC的高,
∵∠ACB=120°,∴∠ACD=60°,在直角三角形ADC中,AD=ACsin60°=1×
.
又S△BMC=S四边形PCBM-S△MPC=
(PM+BC)•PC-
PM•PC
=
(1+2)×1-
×1×1=1
∴VB-MAC=VA-MBC=
S△MBC•AD=
∴三棱锥B-MAC的体积为
.
∴PC⊥平面ABC,
∵AC?平面ABC,∴PC⊥AC.
(II)解:∵PC⊥平面ABC,PC?平面PCBM,∴平面PCBM⊥平面ABC,
如图,
 在平面ABC中过A作AD垂直于BC的延长线与D,则AD⊥平面PCBM,则AD为三棱锥A-MBC的高,
在平面ABC中过A作AD垂直于BC的延长线与D,则AD⊥平面PCBM,则AD为三棱锥A-MBC的高,∵∠ACB=120°,∴∠ACD=60°,在直角三角形ADC中,AD=ACsin60°=1×
| ||
| 2 |
又S△BMC=S四边形PCBM-S△MPC=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
∴VB-MAC=VA-MBC=
| 1 |
| 3 |
| ||
| 6 |
∴三棱锥B-MAC的体积为
| ||
| 6 |
点评:本题主要考查了直线与平面、平面与平面垂直的判定和性质,考查三棱锥B-MAC的体积的计算,考查考查空间想象能力、运算能力和推理论证能力,属于中档题.

练习册系列答案
相关题目
过点P(2,
)作双曲线y=
的切线,则此切线的斜率等于( )
| 1 |
| 2 |
| 1 |
| x |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
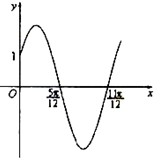 已知函数f(x)=Asin(ωx+φ)(x∈R,ω>0,0<ω<
已知函数f(x)=Asin(ωx+φ)(x∈R,ω>0,0<ω<| π |
| 2 |
A、f(x)=2sin(2x+
| ||
B、f(x)=2sin(2x+
| ||
C、f(x)=2sin(2x-
| ||
D、f(x)=2sin(2x-
|
顶点在原点,坐标轴为对称轴的抛物线过点(-2,3),则它的方程是( )
A、x2=
| ||||
B、x2=±8y或x2=
| ||||
C、x2=
| ||||
D、y2=-
|
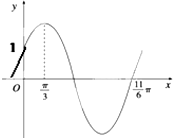 已知函数f(x)=Asin(ωx+φ)(ω>0,0<φ<
已知函数f(x)=Asin(ωx+φ)(ω>0,0<φ<