题目内容
过点P（2，
）作双曲线y=
的切线，则此切线的斜率等于（ ）
| 1 |
| 2 |
| 1 |
| x |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
考点：利用导数研究曲线上某点切线方程
专题：导数的综合应用
分析：求出函数的导数，利用导数的几何意义即可得到结论．
解答：
解：∵y=
，
∴函数的导数为y′=f′(x)=-
，
当x=2时，f′（2）=-
，
则切线的斜率等于f′（2）=-
，
故选：A．
| 1 |
| x |
∴函数的导数为y′=f′(x)=-
| 1 |
| x2 |
当x=2时，f′（2）=-
| 1 |
| 4 |
则切线的斜率等于f′（2）=-
| 1 |
| 4 |
故选：A．
点评：本题主要考查导数的几何意义，求函数的导数是解决本题的关键．
练习册系列答案
相关题目
圆台母线与底面成45°角，侧面积为3
π，则它的轴截面面积是（ ）
| 2 |
| A、2 | ||
| B、3 | ||
C、
| ||
D、3
|
已知平面内两定点A（-5，0），B（5，0），动点M满足|MA|-|MB|=10，则点M的轨迹是（ ）
| A、两条射线 | B、双曲线 |
| C、一条射线 | D、双曲线的一支 |
已知x＞0，y＞0，且2x+y=1，则
+
的最小值是（ ）
| 1 |
| x |
| 2 |
| y |
| A、8 | B、6 | C、3 | D、2 |
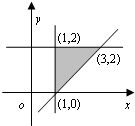已知点（x，y）在如图所示的平面区域（阴影部分）内运动，则z=x2+y2的最大值是（ ）| A、1 | B、3 | C、5 | D、13 |
在等比数列{an}中，如果a1=2，公比q=2，则a4的值为（ ）
| A、4 | B、16 | C、8 | D、32 |
设f（x）=2x，则f（x）的一个原函数是（ ）
| A、x3 | ||
| B、x2-1 | ||
C、
| ||
| D、2x+c |
下列说法错误的是（ ）
| A、一个平面内有两条直线与另外一个平面平行，则这两个平面平行 |
| B、一个平面内任何直线都与另外一个平面平行，则这两个平面平行 |
| C、一个平面内两条相交直线与另外一个平面平行，则这两个平面平行 |
| D、垂直于同一个平面的两条直线平行 |
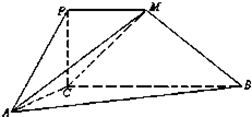如图，四边形PCBM是直角梯形，∠PCB=90°，PM∥BC，PM=1，BC=2．又AC=1，∠ACB=120°，AB⊥PC，直线AM与直线PC所成的角为60°．