题目内容
顶点在原点,坐标轴为对称轴的抛物线过点(-2,3),则它的方程是( )
A、x2=
| ||||
B、x2=±8y或x2=
| ||||
C、x2=
| ||||
D、y2=-
|
考点:抛物线的标准方程
专题:计算题,圆锥曲线的定义、性质与方程
分析:由题意可得,可设抛物线的方程为 x2=2py,或 y2=-2px,p>0,把点(-2,3)代入方程求得p的值,即可求得抛物线的方程.
解答:
解:(1)抛物线的顶点在坐标原点,对称轴是x轴,并且经过点 (-2,3),
设它的标准方程为y2=2px(p>0)
∴9=-4p,解得p=-
,
∴y2=-
x.
(2)抛物线的顶点在坐标原点,对称轴是y轴,并且经过点 (-2,3),
设它的标准方程为x2=-2py(p>0)
∴4=-6p,
解得:p=
.
∴x2=-
y
故选A.
设它的标准方程为y2=2px(p>0)
∴9=-4p,解得p=-
| 9 |
| 4 |
∴y2=-
| 9 |
| 2 |
(2)抛物线的顶点在坐标原点,对称轴是y轴,并且经过点 (-2,3),
设它的标准方程为x2=-2py(p>0)
∴4=-6p,
解得:p=
| 2 |
| 3 |
∴x2=-
| 4 |
| 3 |
故选A.
点评:本题主要考查求抛物线的标准方程的方法,体现了分类讨论的数学思想,属于中档题.

练习册系列答案
相关题目
已知x>0,y>0,且2x+y=1,则
+
的最小值是( )
| 1 |
| x |
| 2 |
| y |
| A、8 | B、6 | C、3 | D、2 |
下列说法错误的是( )
| A、一个平面内有两条直线与另外一个平面平行,则这两个平面平行 |
| B、一个平面内任何直线都与另外一个平面平行,则这两个平面平行 |
| C、一个平面内两条相交直线与另外一个平面平行,则这两个平面平行 |
| D、垂直于同一个平面的两条直线平行 |
∫
(cos
x+
)dx的值为( )
2 0 |
| π |
| 2 |
| 4-x2 |
| A、2π | ||
| B、π | ||
| C、π+1 | ||
D、π+
|
若α,β为锐角,cos(α+β)=
,cos(2α+β)=
,则cosα的值为( )
| 12 |
| 13 |
| 3 |
| 5 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、以上都不对 |
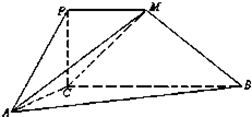 如图,四边形PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=1,BC=2.又AC=1,∠ACB=120°,AB⊥PC,直线AM与直线PC所成的角为60°.
如图,四边形PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=1,BC=2.又AC=1,∠ACB=120°,AB⊥PC,直线AM与直线PC所成的角为60°.