题目内容
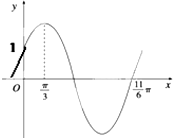 已知函数f(x)=Asin(ωx+φ)(ω>0,0<φ<
已知函数f(x)=Asin(ωx+φ)(ω>0,0<φ<| π |
| 2 |
(Ⅰ)求f(x)的解析式;
(Ⅱ)将函数y=f(x)的图象上所有点的纵坐标不变,横坐标缩短为原来的
| 1 |
| 2 |
| π |
| 6 |
考点:函数y=Asin(ωx+φ)的图象变换,三角函数中的恒等变换应用
专题:三角函数的图像与性质
分析:(Ⅰ)由周期求出ω,由五点法作图求出φ的值,再把(0,1)代入函数的解析式求得A的值,可得函数f(x)的解析式.
(Ⅱ)由题意根据函数y=Asin(ωx+φ)的图象变换规律求得g(x)的解析式,令2kπ-
≤2x-
≤2kπ+
,求得x的范围,可得g(x)的增区间.
(Ⅱ)由题意根据函数y=Asin(ωx+φ)的图象变换规律求得g(x)的解析式,令2kπ-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
解答:
解:(Ⅰ)根据f(x)的图象可得
T=
×
=
-
,∴ω=1.
根据五点法作图可得 1×
+φ=
,求得 φ=
.
再把(0,1)代入函数的解析式可得 Asin
=1,求得A=2,故f(x)=2sin(x+
).
(Ⅱ)将函数y=f(x)的图象上所有点的纵坐标不变,横坐标缩短为原来的
倍,
可得y=2sin(2x+
)的图象;
再将所得函数图象向右平移
个单位,得到函数y=g(x)=2sin[2(x-
)+
]=2sin(2x-
)的图象.
令2kπ-
≤2x-
≤2kπ+
,求得 kπ-
≤x≤kπ+
,
故g(x)的增区间为[kπ-
,kπ+
],k∈z.
| 3 |
| 4 |
| 3 |
| 4 |
| 2π |
| ω |
| 11π |
| 6 |
| π |
| 3 |
根据五点法作图可得 1×
| π |
| 3 |
| π |
| 2 |
| π |
| 6 |
再把(0,1)代入函数的解析式可得 Asin
| π |
| 6 |
| π |
| 6 |
(Ⅱ)将函数y=f(x)的图象上所有点的纵坐标不变,横坐标缩短为原来的
| 1 |
| 2 |
可得y=2sin(2x+
| π |
| 6 |
再将所得函数图象向右平移
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
令2kπ-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
| π |
| 3 |
故g(x)的增区间为[kπ-
| π |
| 6 |
| π |
| 3 |
点评:本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,函数y=Asin(ωx+φ)的图象变换规律,正弦函数的单调性,属于基础题.

练习册系列答案
相关题目
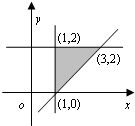 已知点(x,y)在如图所示的平面区域(阴影部分)内运动,则z=x2+y2的最大值是( )
已知点(x,y)在如图所示的平面区域(阴影部分)内运动,则z=x2+y2的最大值是( )| A、1 | B、3 | C、5 | D、13 |
已知数列{an}为等差数列,且a3+a9=20,则S11=( )
| A、110 | B、220 |
| C、200 | D、55 |
若α,β为锐角,cos(α+β)=
,cos(2α+β)=
,则cosα的值为( )
| 12 |
| 13 |
| 3 |
| 5 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、以上都不对 |
不等式(x-2)(x+5)>0的解集为( )
| A、{x|-5<x<2} |
| B、{x|x<-2或x>5} |
| C、{x|-2<x<5} |
| D、{x|x<-5或x>2} |
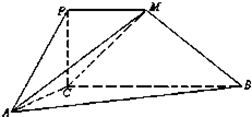 如图,四边形PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=1,BC=2.又AC=1,∠ACB=120°,AB⊥PC,直线AM与直线PC所成的角为60°.
如图,四边形PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=1,BC=2.又AC=1,∠ACB=120°,AB⊥PC,直线AM与直线PC所成的角为60°.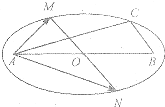 在△ABC中,CA=3CB,cosC=-
在△ABC中,CA=3CB,cosC=-