题目内容
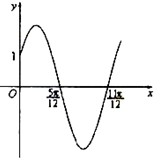已知函数f（x）=Asin（ωx+φ）（x∈R，ω＞0，0＜ω＜| π |
| 2 |
A、f（x）=2sin（2x+
| ||
B、f（x）=2sin（2x+
| ||
C、f（x）=2sin（2x-
| ||
D、f（x）=2sin（2x-
|
考点：由y=Asin（ωx+φ）的部分图象确定其解析式
专题：三角函数的图像与性质
分析：由周期求出ω，由五点法作图求出φ的值，根据图象经过特殊点求得A的值，从而得到函数的解析式．
解答：
解：由
=
•
=
-
，求得ω=2．
根据五点法作图可得 2×
+φ=π，求得φ=
．
再把点（0，1）代入可得Asin
=1，求得A=2，
故函数的解析式为 f（x）=2sin（2x+
），
故选：A．
| T |
| 2 |
| 1 |
| 2 |
| 2π |
| ω |
| 11π |
| 12 |
| 5π |
| 12 |
根据五点法作图可得 2×
| 5π |
| 12 |
| π |
| 6 |
再把点（0，1）代入可得Asin
| π |
| 6 |
故函数的解析式为 f（x）=2sin（2x+
| π |
| 6 |
故选：A．
点评：本题主要考查由函数y=Asin（ωx+φ）的部分图象求解析式，由周期求出ω，由五点法作图求出φ的值，根据图象经过特殊点求得A的值，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
已知平面内两定点A（-5，0），B（5，0），动点M满足|MA|-|MB|=10，则点M的轨迹是（ ）
| A、两条射线 | B、双曲线 |
| C、一条射线 | D、双曲线的一支 |
设f（x）=2x，则f（x）的一个原函数是（ ）
| A、x3 | ||
| B、x2-1 | ||
C、
| ||
| D、2x+c |
下列说法错误的是（ ）
| A、一个平面内有两条直线与另外一个平面平行，则这两个平面平行 |
| B、一个平面内任何直线都与另外一个平面平行，则这两个平面平行 |
| C、一个平面内两条相交直线与另外一个平面平行，则这两个平面平行 |
| D、垂直于同一个平面的两条直线平行 |
已知数列{an}为等差数列，且a3+a9=20，则S11=（ ）
| A、110 | B、220 |
| C、200 | D、55 |
∫
（cos
x+
）dx的值为（ ）
2 0 |
| π |
| 2 |
| 4-x2 |
| A、2π | ||
| B、π | ||
| C、π+1 | ||
D、π+
|
若α，β为锐角，cos（α+β）=
，cos（2α+β）=
，则cosα的值为（ ）
| 12 |
| 13 |
| 3 |
| 5 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、以上都不对 |
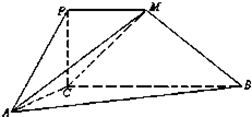如图，四边形PCBM是直角梯形，∠PCB=90°，PM∥BC，PM=1，BC=2．又AC=1，∠ACB=120°，AB⊥PC，直线AM与直线PC所成的角为60°．