题目内容
16.某公司要推出一种新产品,分6个相等时长的时段进行试销,并对卖出的产品进行跟踪以及收集顾客的评价情况(包括产品评价和服务评价),在试销阶段共卖出了480件,通过对所卖出产品的评价情况和销量情况进行统计,一方面发现对该产品的好评率为$\frac{5}{6}$,对服务的好评率为0.75,对产品和服务两项都没有好评有30件,另一方面发现销量和单价有一定的线性相关关系,具体数据如下表:| 时段 | 1 | 2 | 3 | 4 | 5 | 6 |
| 单价x(元) | 800 | 820 | 840 | 860 | 880 | 900 |
| 销量y(件) | 90 | 84 | 83 | 80 | 75 | 68 |
(2)该产品的成本是500元/件,预计在今后的销售中,销量和单价仍然服从这样的线性相关关系($\widehat{y}$=$\widehat{b}$x+$\widehat{a}$),该公司如果想获得最大利润,此产品的定价应为多少元?
(参考公式:线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$中系数计算公式分别为:$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$;K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d)
(参考数据
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
分析 (1)由题意得到2×2列联表,由公式求出K2的观测值,对比参考表格得结论;
(2)求出样本的中心点坐标,计算回归方程的系数,写出利润函数w的解析式,求出w(x)的最大值以及对应的x的值.
解答 解:(1)由题意可得产品好评和服务好评的2×2列联表:
| 服务好评 | 服务没有好评 | 总计 | |
| 产品好评 | 310 | 90 | 400 |
| 产品没有好评 | 50 | 30 | 80 |
| 总计 | 360 | 120 | 480 |
代入K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,得K2=8<10.828.
∴不能在犯错误的概率不超过0.001的前提下,认为产品好评和服务好评有关;
(2)设获得的利润为w元,根据计算可得,$\overline{x}$=850,$\overline{y}=80$,代入入回归方程得,$\widehat{y}=-0.2x+250$.
∴w=(-0.2x+250)(x-500)=-0.2x2+350x-125000.
此函数图象为开口向下,对称轴方程为x=875,
∴当x=875时,w(x)取的最大值.
即该公司如果想获得最大利润,此产品的定价应为875元.
点评 本题考查独立性检验及线性回归方程,考查学生的计算能力,关键是对题意的理解,是中档题.

练习册系列答案
相关题目
14.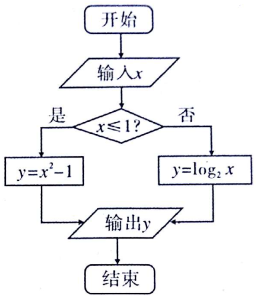 已知如图所示的程序框图的输入值x∈[-1,4],则输出y值的取值范围是( )
已知如图所示的程序框图的输入值x∈[-1,4],则输出y值的取值范围是( )
 已知如图所示的程序框图的输入值x∈[-1,4],则输出y值的取值范围是( )
已知如图所示的程序框图的输入值x∈[-1,4],则输出y值的取值范围是( )| A. | [0,2] | B. | [-1,2] | C. | [-1,15] | D. | [2,15] |
11.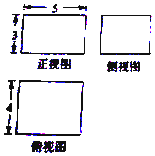 一个四棱柱的三视图如图所示,若该四棱柱的所有顶点都在同一球面上,则这个球的表面积为( )
一个四棱柱的三视图如图所示,若该四棱柱的所有顶点都在同一球面上,则这个球的表面积为( )
 一个四棱柱的三视图如图所示,若该四棱柱的所有顶点都在同一球面上,则这个球的表面积为( )
一个四棱柱的三视图如图所示,若该四棱柱的所有顶点都在同一球面上,则这个球的表面积为( )| A. | 25π | B. | 50π | C. | 100π | D. | 200π |
5.下列命题中,错误的是( )
| A. | ?x∈(0,$\frac{π}{2}$),x>sinx | |
| B. | 在△ABC中,若A>B,则sinA>sinB | |
| C. | 函数f(x)=tanx图象的一个对称中心是($\frac{π}{2}$,0) | |
| D. | ?x0∈R,sinx0cosx0=$\frac{\sqrt{2}}{2}$ |
6.已知抛物线C:y2=4x,过焦点F且斜率为$\sqrt{3}$的直线与C相交于P,Q两点,且P,Q两点在准线上的投影分别为M,N两点,则S△MFN=( )
| A. | $\frac{8}{3}$ | B. | $\frac{{8\sqrt{3}}}{3}$ | C. | $\frac{16}{3}$ | D. | $\frac{{16\sqrt{3}}}{3}$ |