题目内容
5．已知抛物线y2=2px（p＞0）经过点A（1，$\frac{1}{2}$），则它的准线方程为（ ）| A． | x=-$\frac{1}{32}$ | B． | x=-$\frac{1}{16}$ | C． | y=-$\frac{1}{32}$ | D． | y=-$\frac{1}{16}$ |
分析 将点A（1，$\frac{1}{2}$）代入，求出p值，进而根据抛物线的性质，可得准线方程．
解答 解：∵抛物线y2=2px（p＞0）经过点A（1，$\frac{1}{2}$），
∴$\frac{1}{4}$=2p，
解得：p=$\frac{1}{8}$，
故抛物线y2=$\frac{1}{4}$x的准线方程为x=-$\frac{1}{16}$，
故选：B．
点评 本题考查的知识点是抛物线的简单性质，抛物线的标准方程，难度中档．
练习册系列答案
相关题目
10．某连续经营公司的5个零售店某月的销售额和利润资料如表：
（1）若销售额和利润额具有线性相关关系，用最小二乘法计算利润额y对销售额x的回归直线方程；
（2）若该连锁经营公司旗下的某商店F次月的销售额为1亿3千万元，试用（1）中求得的回归方程，估测其利润．（精确到百万元）
参考公式：$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$，$\widehat{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$．
| 商店名称 | A | B | C | D | E |
| 销售额（x）/千万元 | 3 | 5 | 6 | 7 | 9 |
| 利润（y）/百万元 | 2 | 3 | 3 | 4 | 5 |
（2）若该连锁经营公司旗下的某商店F次月的销售额为1亿3千万元，试用（1）中求得的回归方程，估测其利润．（精确到百万元）
参考公式：$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$，$\widehat{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$．
17．
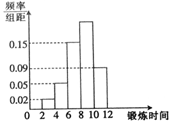某校有150位教职员工，其每周用于锻炼身体所用时间的频率分布直方图如图所示，据图估计，锻炼时间在[8，10）小时内的人数为（ ）
某校有150位教职员工，其每周用于锻炼身体所用时间的频率分布直方图如图所示，据图估计，锻炼时间在[8，10）小时内的人数为（ ）| A． | 30 | B． | 120 | C． | 57 | D． | 93 |
14．已知cosθ＞0，tan（θ+$\frac{π}{4}$）=$\frac{1}{3}$，则θ在（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
15．设函数f（x）=$\left\{\begin{array}{l}{{x}^{2}，x≤1}\\{{2}^{-x}，x＞1}\end{array}\right.$，则f（f（2））=（ ）
| A． | $\frac{1}{16}$ | B． | 16 | C． | $\frac{1}{4}$ | D． | 4 |