题目内容
20．如图，边长为2的正三角形ABC放置在平面直角坐标系xOy中，AC在x轴上，顶点B与y轴上的定点P重合．将正三角形ABC沿x轴正方向滚动，即先以顶点C为旋转中心顺时针旋转，当顶点B落在x轴上时，再以顶点B为旋转中心顺时针旋转，如此继续．当△ABC滚动到△A1B1C1时，顶点B运动轨迹的长度为$\frac{8π}{3}$；在滚动过程中，$\overrightarrow{OB}$•$\overrightarrow{OP}$的最大值为2$\sqrt{3}$．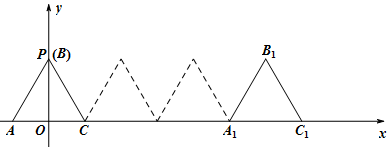
分析 由题意便可知道，点B的轨迹为两个圆心角都为$\frac{2π}{3}$的圆弧和一个点，这样即可求出点B的轨迹长度，分别求出点B在滚动前后的纵坐标的最大值，并求出P（$0，\sqrt{3}$），这样即可求出$\overrightarrow{OB}•\overrightarrow{OP}$的最大值．
解答 解：根据题意知，点B的轨迹为两个圆心角为$\frac{2π}{3}$所对的圆弧和一个点；
且圆弧的半径为2；
∴顶点B运动轨迹的长度为$2•2•\frac{2π}{3}=\frac{8π}{3}$；
$\overrightarrow{OP}=（0，\sqrt{3}）$，设B（x，y）；
①没滚动前点B坐标$（0，\sqrt{3}）$；
∴$\overrightarrow{OB}•\overrightarrow{OP}=3$；
②第一次滚动后B点纵坐标y≤2；
∴$\overrightarrow{OB}•\overrightarrow{OP}≤2\sqrt{3}$；
③第二次滚动后B点坐标（3，0）；
∴$\overrightarrow{OB}•\overrightarrow{OP}=0$；
④第三次滚动后B点纵坐标y≤2；
∴$\overrightarrow{OB}•\overrightarrow{OP}≤2\sqrt{3}$；
∴$\overrightarrow{OB}•\overrightarrow{OP}$的最大值为$2\sqrt{3}$．
故答案为：$\frac{8π}{3}，2\sqrt{3}$．
点评 考查弧长公式，运用坐标解决向量问题的方法，以及数量积的坐标运算．
练习册系列答案
相关题目
5．已知抛物线y2=2px（p＞0）经过点A（1，$\frac{1}{2}$），则它的准线方程为（ ）
| A． | x=-$\frac{1}{32}$ | B． | x=-$\frac{1}{16}$ | C． | y=-$\frac{1}{32}$ | D． | y=-$\frac{1}{16}$ |
夏威夷木瓜是木瓜类的名优品种，肉红微味甜深受市民喜爱．某果农选取一片山地种植夏威夷木瓜，收获时，该果农随机选取果树20株作为样本测量它们每一株的果实产量（单位：kg），获得的所有数据按照区间（40，45]，（45，50]，（50，55]，（55，60]进行分组，得到频率分布直方图如图．已知样本中产量在区间（45，50]上的果树株数是产量在区间（50，60]上的果树株数的$\frac{4}{3}$倍．