题目内容
16.已知△ABC的面积是4,∠BAC=120°,点P满足$\overrightarrow{BP}$=3$\overrightarrow{PC}$,过点P作边AB,AC所在直线的垂线,垂足分别是M,N.则$\overrightarrow{PM}$•$\overrightarrow{PN}$=$\frac{3\sqrt{3}}{8}$.分析 不妨令△ABC为等腰三角形,根据三角形的面积公式求出b2=c2=$\frac{16}{\sqrt{3}}$,再由余弦定理求出a2=16$\sqrt{3}$,再根据投影的定义可的,|$\overrightarrow{PM}$|=$\frac{3a}{8}$,|$\overrightarrow{PN}$|=$\frac{a}{8}$,
最后根据向量的数量积公式计算即可.
解答 解:不妨令△ABC为等腰三角形,∵∠BAC=120°,
∴B=C=30°,
∴b=c,
∴S△ABC=$\frac{1}{2}$bcsinA=4,
∴b2=c2=$\frac{16}{\sqrt{3}}$,
由余弦定理可得a2=b2+c2-2bccosA=$\frac{48}{\sqrt{3}}$=16$\sqrt{3}$,
∵$\overrightarrow{BP}$=3$\overrightarrow{PC}$,
∴|$\overrightarrow{PC}$|=$\frac{1}{4}$|$\overrightarrow{BC}$|=$\frac{a}{4}$,|$\overrightarrow{BP}$|=$\frac{3}{4}$|$\overrightarrow{BC}$|=$\frac{3a}{4}$,
∵过点P作边AB,AC所在直线的垂线,垂足分别是M,N,
∴|$\overrightarrow{PM}$|=|$\overrightarrow{BP}$|•sinB=$\frac{3a}{8}$,|$\overrightarrow{PN}$|=|$\overrightarrow{PC}$|sinC=$\frac{a}{8}$,
∵∠MPN=180°-A=60°,
∴$\overrightarrow{PM}$•$\overrightarrow{PN}$=|$\overrightarrow{PM}$|•|$\overrightarrow{PN}$|cos6°=$\frac{3a}{8}$•$\frac{a}{8}$•$\frac{1}{2}$=$\frac{3{a}^{2}}{128}$=$\frac{3\sqrt{3}}{8}$,
故答案为:$\frac{3\sqrt{3}}{8}$
点评 本题考查了余弦定理三角形的面积公式向量的投影的定义和向量的数量积公式,属于难题.

 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案| A. | {1} | B. | {1,3} | C. | {-1} | D. | {-1,3} |
| A. | {-1,2,2} | B. | {1,2} | C. | {4} | D. | {x|-1≤x≤2} |
| A. | x=-$\frac{1}{32}$ | B. | x=-$\frac{1}{16}$ | C. | y=-$\frac{1}{32}$ | D. | y=-$\frac{1}{16}$ |
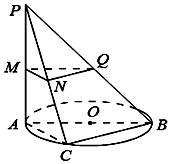 如图,⊙O在平面α内,AB是⊙O的直径,PA⊥平面α,C为圆周上不同于A、B的任意一点,M,N,Q分别是PA,PC,PB的中点.
如图,⊙O在平面α内,AB是⊙O的直径,PA⊥平面α,C为圆周上不同于A、B的任意一点,M,N,Q分别是PA,PC,PB的中点.